Basic Math & Pre-Algebra All-in-One For Dummies (+ Chapter Quizzes Online)
Explore Book Buy On AmazonFor example, the idea of Tetris is to manoeuvre different-shaped blocks falling from above into a rectangular space – any time you complete a line all the way across without any gaps, the line disappears and the blocks above it shift down.
Tetris is all about tessellation: fitting shapes together so there aren’t any gaps. Some other places you see tessellation are in the work of Dutch artist M.C. Escher and in a great deal of Islamic art – for instance at the Alhambra Palace in Spain.
You don’t need to think of tessellation in quite the same depth as these artists – although it can be fun to do so. For the numeracy curriculum, you only need to worry about fairly regular shapes. By the way, tessellation is part of the syllabus, but setting multiple-choice questions on tessellation is very hard, so it doesn’t often come up in the exam.
Tessellation has one important rule: wherever lines meet, the angles have to add up to 360 degrees.
Tetris works because the corners on all of the shapes are 90-degree angles, and when four of the shapes meet you end up with no spaces. Not only 90-degree angles tessellate, though. To give just a few examples, you can also tile equilateral triangles (with 60-degree corners) and hexagons (six sides and 120-degree corners).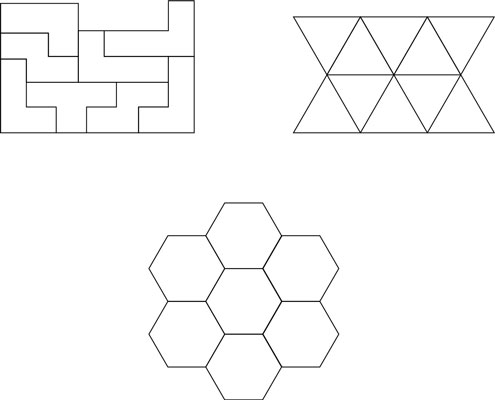
The only kind of multiple-choice question that would involve tessellation involves ‘filling in the gap’ – the examiner gives you two or three shapes that meet at a corner and you need to find the angle on the remaining shape.
This is a pretty simple process if you remember the important rule that I mention above: wherever lines meet, the angles have to add up to 360 degrees.
-
Write down the size of each angle touching the corner you’re interested in.
-
Add up all the angles from Step 1.
-
You need to make 360 degrees in the corner. Work out: 360 take away the angle you worked out in Step 2. The answer is the size of the angle you need to put in the corner.

