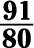Fractions represent parts of a whole — that is, quantities that fall between the whole numbers. Probably the most commonly used fraction is 1/2, which is one-half. When you cut a cake into two pieces and take one for yourself, you get 1/2 of the cake —hope you're hungry!

When you slice yourself a fraction of a cake, that fraction contains two numbers, and each number tells you something different:
The top number — called the numerator — tells you the number of shaded slices.
The bottom number — called the denominator — tells you the total number of slices.
When the numerator of a fraction is less than the denominator, that fraction is a proper fraction. If the numerator is greater than the denominator, that fraction is an improper fraction. You can convert improper fractions into mixed numbers.
Some fractions can be easily written as whole numbers:
When a fraction's denominator is 1, that fraction is equal to its numerator.
When a fraction's numerator and denominator are the same, that fraction is equal to 1. (This idea is important when you want to change the terms of a fraction.)
When you reverse the order of the numerator and denominator in a fraction, the result is the reciprocal of that fraction. You use reciprocals to divide by fractions.
Sample questions
For each cake pictured below, identify the fraction of the cake that’s shaded.
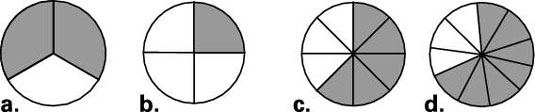
Put the number of shaded slices over the number of total slices in each cake:
a.
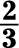
b.
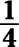
c.
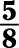
d.
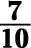
What’s the reciprocal of each of the following fractions?
a.
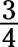
b.
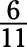
c.
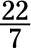
d.
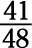
To find the reciprocal, switch around the numerator and the denominator:
a. The reciprocal is
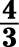
b. The reciprocal is
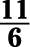
c. The reciprocal is
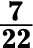
d. The reciprocal is
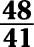
Practice questions
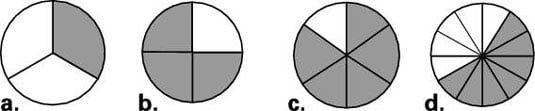
For each cake pictured, identify the fraction of the cake that’s shaded.
Which of the following fractions are proper? Which are improper?
a.
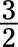
b.
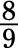
c.
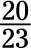
d.
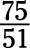
Rewrite each of the following fractions as a whole number:
a.
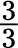
b.
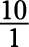
c.
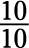
d.
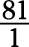
Find the reciprocal of the following fractions:
a.
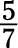
b.
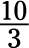
c.
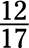
d.
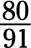
Following are the answers to the practice questions:
Identify the fraction of the cake that’s shaded.
a. You have 1 shaded slice and 3 slices in total, so it’s
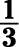
b. You have 3 shaded slices and 4 slices in total, so it’s
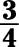
c. You have 5 shaded slices and 6 slices in total, so it’s
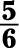
d. You have 7 shaded slices and 12 slices in total, so it’s
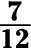
Which of the following fractions are proper? Which are improper?
a. The numerator (3) is greater than the denominator (2), so this fraction is an improper fraction.
b. The numerator (8) is less than the denominator (9), so this fraction is a proper fraction.
c. The numerator (20) is less than the denominator (23), so this fraction is a proper fraction.
d. The numerator (75) is greater than the denominator (51), so this fraction is an improper fraction.
Rewrite each of the following fractions as a whole number.
a. The numerator and denominator are the same, so
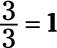
b. The denominator is 1, so
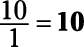
c. The numerator and denominator are the same, so
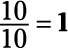
d. The denominator is 1, so
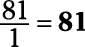
Find the reciprocal of the following fractions by switching the numerator and denominator.
a. The reciprocal is
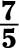
b. The reciprocal is
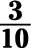
c. The reciprocal is
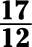
d. The reciprocal is