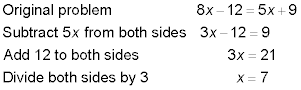The ten little math demons listed here plague all sorts of otherwise smart, capable folks like you. The good news is that they're not as big and scary as you may think, and they can be dispelled more easily than you may have dared believe.
Knowing the multiplication table
A sketchy knowledge of multiplication can really hold back an otherwise good math student. Here's a quick quiz: the ten toughest problems from the multiplication table.
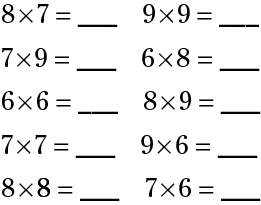
Can you do this, 10 for 10, in 20 seconds? If so, you're a multiplication whiz.
Adding and subtracting negative numbers
It's easy to get confused when adding and subtracting negative numbers. To begin, think of adding a number as moving up and subtracting a number as moving down. For example:
2 + 1 – 6 means up 2, up 1, down 6
So if you go up 2 steps, then up 1 more step, and then down 6 steps, you've gone a total of 3 steps down; therefore, 2 + 1 – 6 = –3.
Here's another example:
–3 + 8 – 1 means down 3, up 8, down 1
This time, go down 3 steps, then up 8 steps, and then down 1 step, you've gone a total of 4 steps up; therefore, –3 + 8 – 1 = 4.
You can turn every problem involving negative numbers into an up-and-down example. The way to do this is by combining adjacent signs:
Combine a plus and minus as a minus sign.
Combine two minus signs as a plus sign.
For example:
–5 + (–3) – (–9)
In this example, you see a plus sign and a minus sign together (between the 5 and the 3), which you can combine as a minus sign. You also see two minus signs (between the 3 and the 9), which you can combine as a plus sign:
–5 – 3 + 9 means down 5, down 3, up 9
This technique allows you to use your up-and-down skills to solve the problem: Down 5 steps, then down 3 steps, and up 9 steps leaves you 1 step up; therefore, –5 + (–3) – (–9) = 1.
Multiply and dividing negative numbers
When you multiply or divide a positive number by a negative number (or vice versa), the answer is always negative. For example:
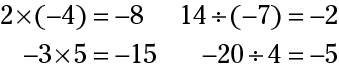
When you multiply two negative numbers, remember this simple rule: Two negatives always cancel each other out and equal a positive.
Knowing the difference between factors and multiples
Lots of students get factors and multiples confused because they're so similar. Both are related to the concept of divisibility. When you divide one number by another and the answer has no remainder, the first number is divisible by the second. For example:
When you know that 12 is divisible by 3, you know two other things as well:
3 is a factor of 12 and 12 is a multiple of 3
In the positive numbers, the factor is always the smaller of the two numbers and the multiple is always the larger.
Reducing fractions to lowest terms
Math teachers usually request (or force!) their students to use the smallest-possible version of a fraction — that is, to reduce fractions to lowest terms.
To reduce a fraction, divide the numerator (top number) and denominator (bottom number) by a common factor, a number that they're both divisible by. For example, 50 and 100 are both divisible by 10, so

The resulting fraction,
can still be further reduced, because both 5 and 10 are divisible by 5:
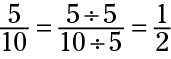
When you can no longer make the numerator and denominator smaller by dividing by a common factor, the result is a fraction that's reduced to lowest terms.
Adding and subtracting fractions
Adding and subtracting fractions that have the same denominator is pretty simple: Perform the operation (adding or subtracting) on the two numerators and keep the denominators the same.
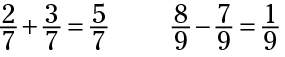
When two fractions have different denominators, you can add or subtract them without finding a common denominator by using cross-multiplication, as shown here:
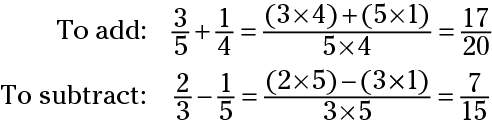
Multiplying and dividing fractions
To multiply fractions, multiply their two numerators to get the numerator of the answer, and multiply their two denominators to get the denominator. For example:
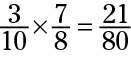
To divide two fractions, turn the problem into multiplication by taking the reciprocal of the second fraction — that is, by flipping it upside down. For example:
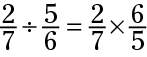
Now multiply the two resulting fractions:
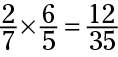
Identifying algebra's main goal: find x
Everything in algebra is, ultimately, for one purpose: Find x (or whatever the variable happens to be). Algebra is really just a bunch of tools to help you do that. You even use algebra to solve word problems that would be much more difficult without algebra to help.
Knowing algebra's main rule: keep the equation in balance
The main idea of algebra is simply that an equation is like a balance scale: Provided that you do the same thing to both sides, the equation stays balanced. For example, consider the following equation:
8x – 12 = 5x + 9
To find x, you can do anything to this equation as long as you do it equally to both sides.
Seeing Algebra's Main Strategy: Isolate x
The best way to find x is to isolate it — that is, get x on one side of the equation with a number on the other side. To do this while keeping the equation balanced requires great cunning and finesse. Here's an example, using the equation from the preceding section: