In geometry, the centroid of a triangle is the point where the medians intersect. The following practice questions ask you to find the coordinates of a centroid in a triangle and to find the distance from one of the vertices to the centroid, given the median length.
Practice questions
Use the given information to solve the practice questions.
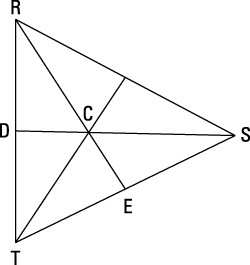
Point C represents the centroid of triangle RST. If SD = 21, find SC.
The vertices of a triangle are (0, –2), (4, 0), and (2, 8). Find the coordinates of the centroid of the triangle.
Answers and explanations
14
The centroid of a triangle divides each median of the triangle into segments with a 2:1 ratio. You don't know the length of either segment of the median, so you'll use an x in the ratio to represent the shorter length.

You're given that SD = 21; therefore,

(2, 2)
You find the centroid of a triangle by averaging the x coordinates and the ycoordinates of all three vertices of the triangle. The average of the x coordinates is

The average of the y coordinates is

Therefore, the centroid of the triangle is (2, 2).





