To solve certain limit problems, you’ll need the conjugate multiplication technique. When substitution doesn’t work in the original function — usually because of a hole in the function — you can use conjugate multiplication to manipulate the function until substitution does work (it works because your manipulation plugs up the hole).
Try this method for fraction functions that contain square roots. Conjugate multiplication rationalizes the numerator or denominator of a fraction, which means getting rid of square roots.
Try substitution.

Multiply the numerator and denominator by the conjugate of the expression containing the square root.
The conjugate of a two-term expression is just the same expression with subtraction switched to addition or vice versa.

The product of conjugates is always the square of the first thing minus the square of the second thing.
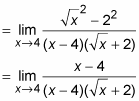
Cancel the (x – 4) from the numerator and denominator.
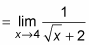
Now substitution works.
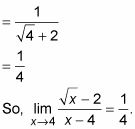
This rationalizing process plugged the hole in the original function.
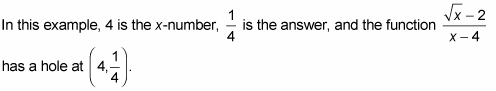
And you see that the answer to the limit problem is the height of the hole.

