Here’s how you integrate a trig integral that contains sines and cosines where the power of sine is odd and positive. You lop off one sine factor and put it to the right of the rest of the expression, convert the remaining (even) sine factors to cosines with the Pythagorean identity, and then integrate with the substitution method where u = cos(x).
Remember that the Pythagorean identity tells you that, for any angle x,
And thus,
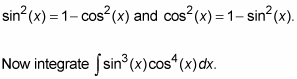
Lop off one sine factor and move it to the right.
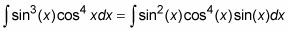
Convert the remaining (even) sines to cosines by using the Pythagorean identity and simplify.
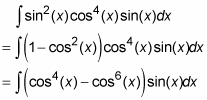
Integrate with substitution, where u = cos(x).
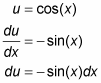
You can save a little time in all substitution problems by just solving for du—as is done immediately above — and not bothering to solve for dx. You then tweak the integral so that it contains the thing du equals (–sin(x)dx in this problem). The integral contains a sin(x)dx, so you multiply it by –1 to turn it into –sin(x)dx and then compensate for that –1 by multiplying the whole integral by –1. This is a wash because –1 times –1 equals 1. This may not sound like much of a shortcut, but it’s a good time saver once you get used to it.
So tweak your integral:
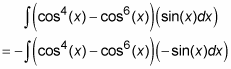
Now substitute and solve by the reverse power rule:
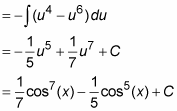
It’s a walk in the park.

