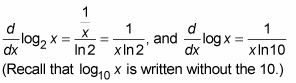Differentiating exponential and logarithmic functions involves special rules. No worries — once you memorize a couple of rules, differentiating these functions is a piece of cake.
Exponential functions: If you can’t memorize this rule, hang up your calculator.

Look at the graph of y = ex in the following figure.
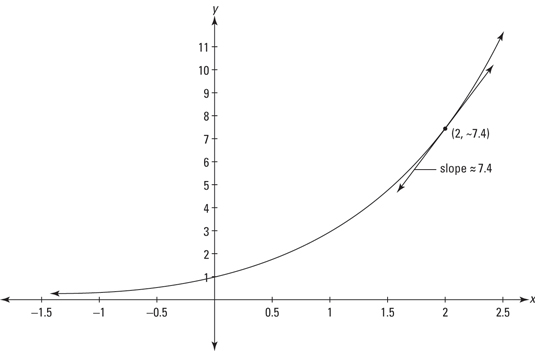
Pick any point on this function, say (2, ~7.4). The height of the function at that point, ~7.4, is the same as the slope at that point.
If the base of the logarithmic function is a number other than e, you have to tweak the derivative by multiplying it by the natural log of the base. Thus,
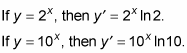
Logarithmic functions: And now — can you guess? — the derivatives of logarithmic functions. Here’s the derivative of the natural log — that’s the log with base e:
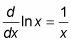
If the log base is a number other than e, you tweak this derivative — like with exponential functions — except that you divide by the natural log of the base instead of multiplying. Thus,