You don’t see many telescoping series, but the telescoping series rule is a good one to keep in your bag of tricks — you never know when it might come in handy. Consider the following series:
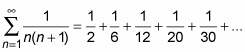
To see that this is a telescoping series, you have to use the partial fractions technique to rewrite
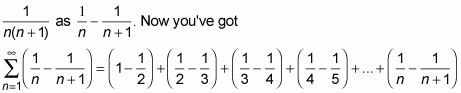
All these terms now collapse, or telescope. The 1/2s cancel, the 1/3s cancel, the 1/4s cancel, and so on. All that’s left is the first term, 1 (actually, it’s only half a term), and the last half-term,
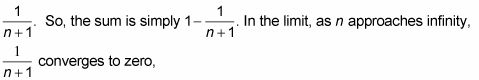
and thus the sum converges to 1 – 0, or 1.
You can write each term in a telescoping series as the difference of two half-terms — call them h-terms. You can then write the telescoping series as
Here's the telescoping series rule: A telescoping series of the above form converges if
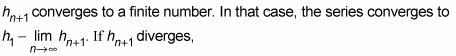
then the series diverges.
This rule, like the rule for geometric series, lets you determine what number a convergent telescoping series converges to.

