Because the Taylor series is a form of power series, every Taylor series also has an interval of convergence. When this interval is the entire set of real numbers, you can use the series to find the value of f(x) for every real value of x.
However, when the interval of convergence for a Taylor series is bounded — that is, when it diverges for some values of x — you can use it to find the value of f(x) only on its interval of convergence.
For example, here are the three important Taylor series:
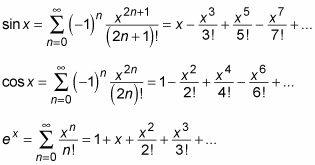
All three of these series converge for all real values of x, so each equals the value of its respective function.
Now consider the following function:
You need to express this function as a Maclaurin series, which takes this form:
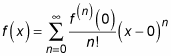
The notation f(n) means “the nth derivative of f.” This becomes clearer in the expanded version of the Maclaurin series:
To do this, follow these steps:
Find the first few derivatives of
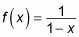
until you recognize a pattern:
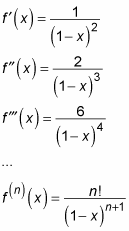
Substitute 0 for x into each of these derivatives:
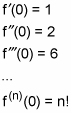
Plug these values, term by term, into the formula for the Maclaurin series:
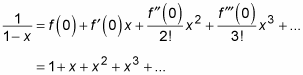
If possible, express the series in sigma notation:
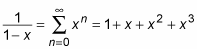
To test this formula, you can use it to find f(x) when
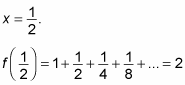
You can test the accuracy of this expression by substituting
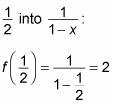
As you can see, the formula produces the correct answer. Now try to use it to find f(x) when x = 5, noting that the correct answer should be
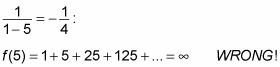
What happened? This series converges only on the interval (–1, 1), so the formula produces only the value f(x) when x is in this interval. When x is outside this interval, the series diverges, so the formula is invalid.

