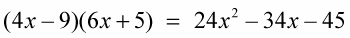UnFOILing is a method for factoring a trinomial into two binomials. When you multiply two binomials together, you use the FOIL method, multiplying the First, then the Outer, then the Inner, and finally the Last terms of the two binomials into a trinomial. But when you need to factor a trinomial, you unFOIL by determining the factor pairs for a and c, the correct signs to place inside the two binomials, and what combination of factor pairs of a and c results in b.
The key to unFOILing is being organized:
Be sure you have an expression in the form:
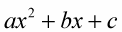
Write the terms in the order of decreasing powers.
Remember how to assign the correct signs in each binomial:
The signs are both positive, if c is positive and b is positive.
The signs are both negative, if c is positive and b is negative.
One sign is positive and one negative, if c is negative; which binomial is positive and which one is negative depends on whether b is positive or negative and how you arranged the factors.
Example:

Determine all the ways you can multiply two numbers to get a.
You can get these numbers from the prime factorization of a. Sometimes, writing out the list of ways to multiply is a big help. In this example, a is 24, and the list of ways you can multiply two numbers to get 24 is:
1 × 24, 2 × 12, 3 × 8, or 4 × 6.
Determine all the ways you can multiply two numbers to get c.
In this example, c is 45, and you can multiply the following numbers to get 45:
1 × 45, 3 × 15, or 5 × 9.
Ignore the sign at this point. You don't need to worry about signs until Step 3.
Look at the sign of c and your lists from Steps 1 and 2 to see if you want a sum or difference.
If c is positive, find a value from your Step 1 list and another from your Step 2 list such that the sum of their product and the product of the two remaining numbers in those steps results in b.
If c is negative, find a value from your Step 1 list and another from your Step 2 list such that the difference of their product and the product of two remaining numbers from those steps results in b.
For the trinomial
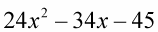
c is negative, so you want a difference of 34 between products.
Choose a product from Step 1 and a product from Step 2 that result in the correct sum or difference determined in Step 3.
Because you determined in Step 3 that you want a difference of 34 between products, use 4 × 6 from a and 5 × 9 from c.
The product of 4 and 5 is 20. The product of 6 and 9 is 54. The difference of these products is 34.
Arrange your choices as binomials so the results are those you want.
(4x 9)(6x 5)
Place the signs to give the desired results.
(4x – 9)(6x + 5)
FOIL the two binomials to check your work.
If the binomials are correct, you'll end up with the original problem when you FOIL them.