Decomposition methods are based on an analysis of the individual components of a time series. The strength of each component is estimated separately and then substituted into a model that explains the behavior of the time series. Two of the more important decomposition methods are
Multiplicative decomposition
Additive decomposition
Multiplicative decomposition
The multiplicative decomposition model is expressed as the product of the four components of a time series:
yt = TRtStCtIt
These variables are defined as follows:
yt = Value of the time series at time t
TRt = Trend at time t
St = Seasonal component at time t
Ct = Cyclical component at time t
It = Irregular component at time t
Each component has a subscript t to indicate a specific time period. The time period can be measured in weeks, months, quarters, years, and so forth.
For example, sales of air conditioners depend heavily on the season of the year; due to population growth, sales of air conditioners also show a positive trend over time. Suppose you use the following equation to estimate (and to explain) the trend in the demand for air conditioners:
TRt = 1000 + 25t
Quarterly data is used, so t represents the time measured in quarters. This equation indicates that over time, sales of air conditioners tend to rise by 25 units per quarter. Using the trend equation, the forecast of air conditioner sales over the coming year looks like this:
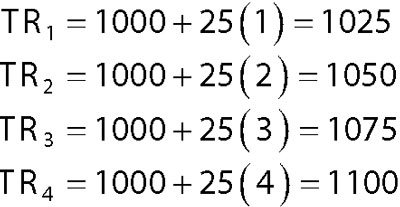
Seasonal factors are handled by giving different weights to each season that are used to adjust the trend components. Assume that the seasonal factors for four seasons are as follows:
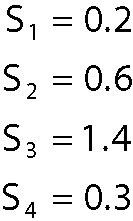
These values show that the seasonal demand for air conditioners is strongest in the third quarter and weakest in the fourth and first quarters. (If there is no seasonal effect, then each of these factors would be equal to 1.) Incorporating the seasonal factors into the model gives the following adjusted forecasts:
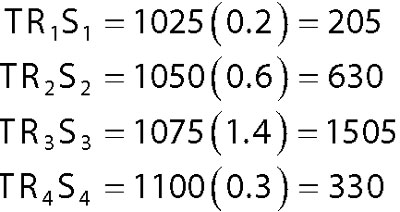
Now, suppose you estimate the four cyclical (quarterly) factors to be:
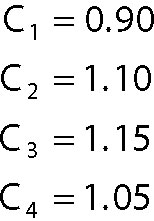
Incorporating the cyclical factors gives the following adjusted forecast for the four quarters over the coming year:

Additive decomposition
With additive decomposition, a time series is modeled as the sum of the trend, seasonal effect, cyclical effect, and irregular effects. This is shown in the following equation:
yt = TRt + St + Ct + It
The additive decomposition method is more appropriate when the seasonal factors tend to be steady from one year to the next. By contrast, multiplicative decomposition is more widely used since many economic time series have a seasonal factor that grows proportionately with the level of the time series. In other words, economic growth tends to be multiplicative rather than linear, because returns are compounded over time.
For example, sales of ice-cream increase more during the summer as the population grows, so the seasonal factor increases over time. In this case, you'd use multiplicative decomposition to forecast the demand for ice-cream.

