An autocorrelation plot shows the properties of a type of data known as a time series. A time series refers to observations of a single variable over a specified time horizon. For example, the daily price of Microsoft stock during the year 2013 is a time series.
Cross-sectional data refers to observations on many variables at a single point in time. For example, the closing prices of the 30 stocks contained in the Dow Jones Industrial Average on January 31, 2014, would be considered cross-sectional data.
An autocorrelation plot is designed to show whether the elements of a time series are positively correlated, negatively correlated, or independent of each other. (The prefix auto means "self"— autocorrelation specifically refers to correlation among the elements of a time series.)
An autocorrelation plot shows the value of the autocorrelation function (acf) on the vertical axis. It can range from –1 to 1.
The horizontal axis of an autocorrelation plot shows the size of the lag between the elements of the time series. For example, the autocorrelation with lag 2 is the correlation between the time series elements and the corresponding elements that were observed two time periods earlier.
This figure shows an autocorrelation plot for the daily prices of Apple stock from January 1, 2013 to December 31, 2013.
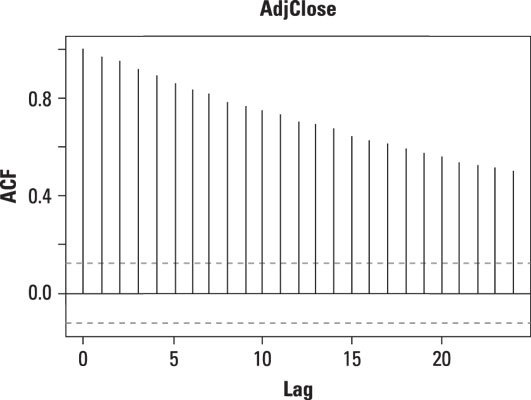
On the graph, there is a vertical line (a "spike") corresponding to each lag. The height of each spike shows the value of the autocorrelation function for the lag.
The autocorrelation with lag zero always equals 1, because this represents the autocorrelation between each term and itself. Price and price with lag zero are the same variable.
Each spike that rises above or falls below the dashed lines is considered to be statistically significant. (Chapter 16 talks about this in detail.) This means the spike has a value that is significantly different from zero. If a spike is significantly different from zero, that is evidence of autocorrelation. A spike that's close to zero is evidence against autocorrelation.
In this example, the spikes are statistically significant for lags up to 24. This means that the Apple stock prices are highly correlated with each other. In other words, when the price of Apple stock rises, it tends to continue rising. When the price of Apple stock falls, it tends to continue falling. This figure illustrates this.
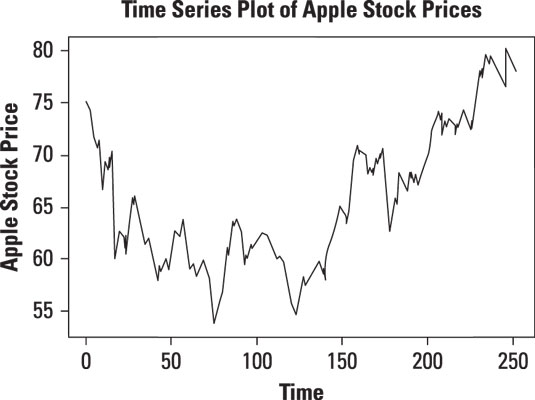
Even though the daily prices of Apple stock are highly correlated, the daily returns may not be. You compute the daily returns from the daily prices as follows:
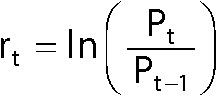
where
rt = The continuously compounded return at time t
Pt = The price at time t
Pt-1 = The price at time t – 1 (one period before t)
ln = The natural logarithm
The natural logarithm is the logarithm with base e, which is approximately equal to 2.71828… .
This figure shows an autocorrelation plot for the daily returns to Apple stock from January 1, 2013 to December 31, 2013.
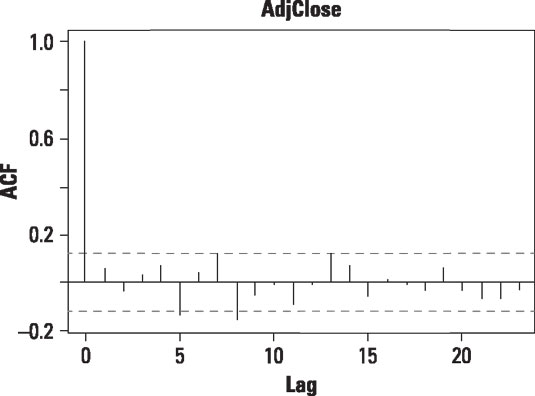
The autocorrelation plot for daily returns to Apple stock shows that most of the spikes are not statistically significant. This indicates that the returns are not highly correlated, as shown here.
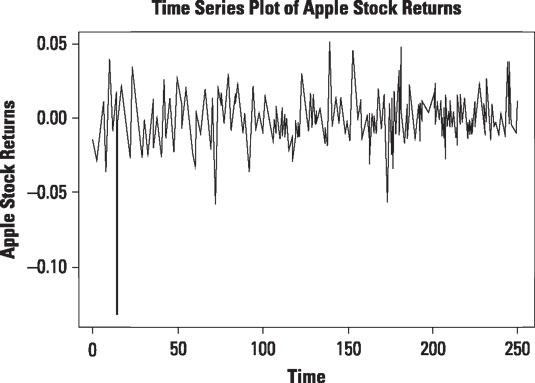
The graph shows that except for one major downturn, the returns to Apple stock between January 1, 2013 and December 31, 2013 do not show any particular pattern — they tend to fluctuate randomly around zero. This means that the returns are largely independent of each other.
You can use an autocorrelation plot to determine whether the elements of a time series are random (that is, unrelated to each other). This is important, because many statistical tests involving time series are based on this assumption.
As you can see, there are many different ways to visualize your data. A picture is worth a thousand words, as the saying goes. And it definitely holds true in data analysis. Statistical software packages generally come equipped with easy-to-use graphical tools. By taking advantage of them, you can quickly gain insight into your data that no amount of number crunching could give you.

