For a dataset that consists of observations taken at different points in time (that is, time series data), it's important to determine whether or not the observations are correlated with each other. This is because many techniques for modeling time series data are based on the assumption that the data is uncorrelated with each other (independent).
One graphical technique you can use to see whether the data is uncorrelated with each other is the autocorrelation function. The autocorrelation function shows the correlation between observations in a time series with different lags. For example, the correlation between observations with lag 1 refers to the correlation between each individual observation and its previous value.
This figure shows the autocorrelation function for ExxonMobil's daily returns in 2013.
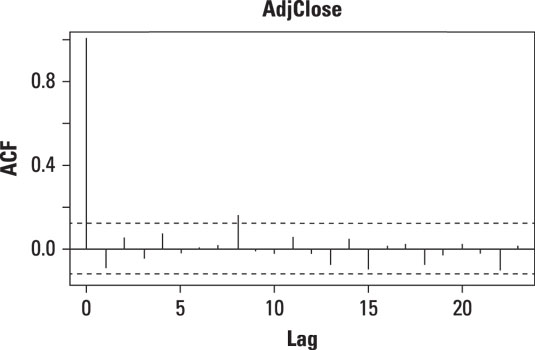
Each "spike" in the autocorrelation function represents the correlation between observations with a given lag.
The autocorrelation with lag 0 always equals 1, because this represents the correlations of the observations with themselves.
On the graph, the dashed lines represent the lower and upper limits of a confidence interval. If a spike rises above the upper limit of the confidence interval or falls below the lower limit of the confidence interval, that shows that the correlation for that lag isn't 0. This is evidence against the independence of the elements in a dataset.
In this case, there is only one statistically significant spike (at lag 8). This spike shows that the ExxonMobil returns may be independent. A more formal statistical test would show whether that is true or not.

