Because it wouldn't be humanly possible to create a table of probabilities and corresponding t-values for every possible t-distribution, statisticians created the t-table, which shows certain values of t-distributions for a selection of degrees of freedom and a selection of probabilities.
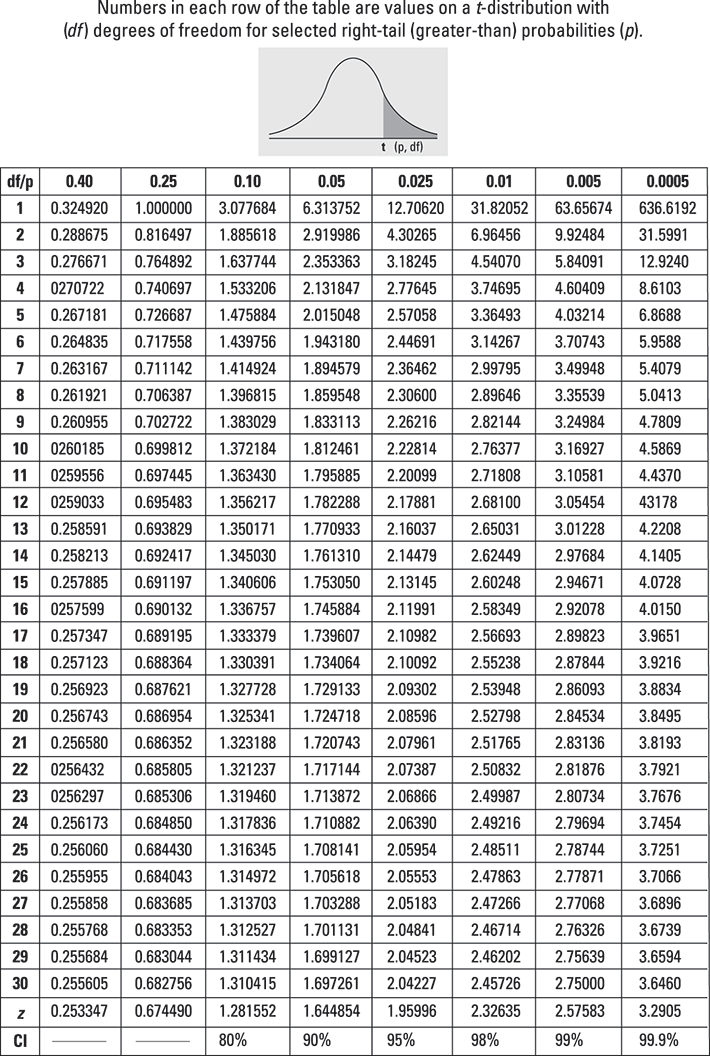
Each row of the t-table represents a different t-distribution, classified by its degrees of freedom (df). The columns represent various common greater-than probabilities, such as 0.40, 0.25, 0.10, and 0.05. The numbers across a row indicate the values on the t-distribution (the t-values) corresponding to the greater-than probabilities shown at the top of the columns. Rows are arranged by degrees of freedom.
Another term for greater-than probability is right-tail probability, which indicates that such probabilities represent areas on the right-most end (tail) of the t-distribution.
For example, the second row of the t-table is for the t2 distribution (2 degrees of freedom, pronounced tee sub-two). You see that the second number, 0.816, is the value on the t2 distribution whose area to its right (its right-tail probability) is 0.25 (see the heading for column 2). In other words, the probability that t2 is greater than 0.816 equals 0.25. In probability notation, that means p(t2 > 0.816) = 0.25.The next number in row two of the t-table is 1.886, which lies in the 0.10 column. This means the probability of being greater than 1.886 on the t2 distribution is 0.10. Because 1.886 falls to the right of 0.816, its right-tail probability is lower.
Follow these steps to use the t-table to find right-tail probabilities and p-values for hypothesis tests involving t:
-
Find the t-value for which you want the right-tail probability (call it t), and find the sample size (for example, n).
-
Find the row corresponding to the degrees of freedom (df) for your problem (for example, n – 1). Go across that row to find the two t-values between which your t falls.
For example, if your t is 1.60 and your n is 7, you look in the row for df = 7 – 1 = 6. Across that row, you find your t lies between t-values 1.44 and 1.94.
-
Go to the top of the columns containing the two t-values from Step 2.
The right-tail (greater-than) probability for your t-value is somewhere between the two values at the top of these columns. For example, your t = 1.60 is between t-values 1.44 and 1.94 (df = 6); so the right tail probability for your t is between 0.10 (column heading for t = 1.44) and 0.05 (column heading for t = 1.94).
The row near the bottom with Z in the df column gives right-tail (greater-than) probabilities from the Z-distribution.
Here's how to use the t-table to find t*-values (critical values) for a confidence interval involving t:-
Determine the confidence level you need (as a percentage).
-
Determine the sample size (for example, n).
-
Look at the bottom row of the table where the percentages are shown.
Find your % confidence level there.
-
Intersect this column with the row representing your degrees of freedom (df).
This is the t-value you need for your confidence interval.
For example, a 95% confidence interval with df = 6 has t * = 2.45. (Find 95% on the last line and go up to row 6.)

