Many real-world scenarios are looking to compare two populations. For example, what is the difference in survival rates for cancer patients taking a new drug compared to cancer patients on the existing drug? What is the difference in the average salary for males versus females? What’s the difference in the average price of gas this year compared to last year?
All these questions are really asking you to compare two populations in terms of either their averages or their proportions to see how much difference exists (if any). The technique you use here is confidence intervals for two populations.
For the following practice questions, consider that: A random poll of 100 males and 100 females who were likely to vote in an upcoming election found that 55% of the males and 25% of the females supported candidate Johnson. Call the population of males “Population 1” and the population of females “Population 2” while working these problems.
Sample questions
If you could use only one number to estimate the difference in the proportions of all males and all females supporting candidate Johnson among all likely voters, what number would you use?
Answer: 0.30
If you could use only one number to estimate the difference between two population proportions, you’d use the difference in the two sample proportions. So calling the population of males Population 1 and the population of females Population 2, for this specific data set from these samples taken from the populations, you get
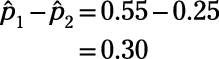
Note, however, that a confidence interval is the best estimate for the difference in two population proportions because you know the sample proportions change as soon as the sample changes, and a confidence interval provides a range of likely values rather than just one number for the population parameter. So using 0.30 plus or minus a margin of error gives you the best possible estimate.
What is the standard error for the estimate of the difference in proportions in the male and female populations?
Answer: 0.0660
To calculate the standard error for the estimated difference in two population proportions, use the formula
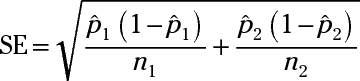
where
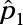
and n1 are the sample proportion and sample size of the sample from Population 1, and
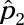
and n2 are the sample proportion and sample size of the sample from Population 2.
Treating the sample of males from Population 1 as Sample 1 and the sample of females from Population 2 as Sample 2, plug in the numbers and solve:

So the standard error for the estimate of the difference in proportions in the male and female populations is 0.0660.
If you need more practice on this and other topics from your statistics course, visit 1,001 Statistics Practice Problems For Dummies to purchase online access to 1,001 statistics practice problems! We can help you track your performance, see where you need to study, and create customized problem sets to master your stats skills.

