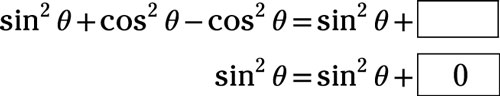Pre-Calculus: 1001 Practice Problems For Dummies (+ Free Online Practice)
Explore Book Buy On AmazonThe basic trig identities will get you through most problems and applications involving trigonometry. But if you’re going to broaden your horizons and study more and more mathematics, you’ll find some additional identities crucial to your success. Also, in some of the sciences, especially physics, these specialized identities come up in the most unlikely (and likely) places.
These trigonometric identities are broken into groups, depending on whether you’re trying to combine angles or split them apart, increase exponents or reduce them, and so on. The groupings can help you to decide which identity to use in which situation. Keep a list of these identities handy, because you’ll want to refer to them as you work through the problems.
You’ll work with the more-advanced trig identities in the following ways:
Using the function values of two angles to determine the function value of the sum of the angles
Applying the identities for the difference between two angles
Making use of the half-angle identities
Working from product-to-sum and sum-to-product identities
Using the periods of functions in identities
Applying power-reducing identities
Deciding which identity to use first
When you’re working on these particular trig identities, some challenges will include the following:
Applying the identities using the correct order of operations
Simplifying the radicals correctly in half-angle identities
Making the correct choices between positive and negative identities
Practice problems
Use a sum or difference identity to determine the missing term in the identity:
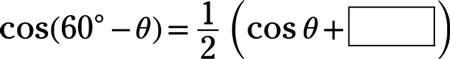
Answer:
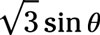
Use the cosine-of-a-difference identity:
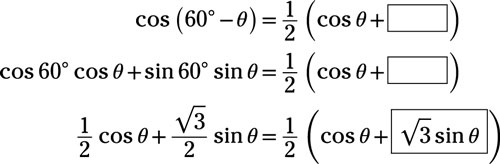
Use a double-angle identity to determine the missing term in the identity.
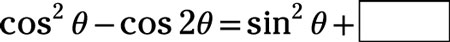
Answer: 0
Replace

with the double-angle identity involving the cosine:
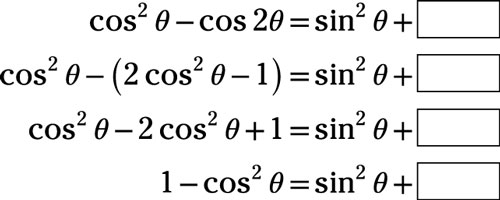
Replace the 1 with
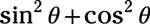
from the Pythagorean identity: