If you want to know whether lines are parallel or perpendicular to each other (or neither), you first need to write their equations in slope-intercept form: y = mx + b.
The following practice geometry questions ask you to rewrite pairs of line equations, and then compare their slopes.
Practice questions
State whether the following two lines are parallel, perpendicular, or neither: 2y + 3 = 4x and 4y + 2x = 12.
State whether the following two lines are parallel, perpendicular, or neither:
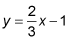
and 6y = 4x + 3.
Answers and explanations
Perpendicular
Lines that are parallel have equal slopes. Perpendicular lines have slopes that are negative reciprocals of each other. To determine the slope of each line, first put the equations in slope-intercept form:
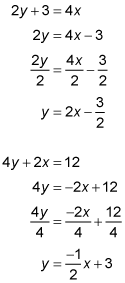
The slope-intercept form of a line is y = mx + b, where m represents the slope and b represents the y-intercept. The first equation shows that the slope of the line is 2. The second equation shows that the slope of the line is
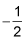
Because the two slopes are negative reciprocals of each other, the lines must be perpendicular.
Parallel
Lines that are parallel have equal slopes. Lines that are perpendicular have slopes that are negative reciprocals of each other. To determine the slope of the second line, put its equation in slope-intercept form:
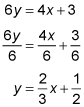
The slope-intercept form of a line is y = mx + b, where m represents the slope and b represents the y-intercept. The first equation shows that the slope of the line is
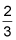
and the second equation shows that the slope of the other line is also
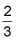
Because the two slopes are equal, the lines must be parallel.

