Common Core math students start to work with exponents in eighth grade. In algebra, you can think of exponentiation as repeated multiplication. The following analogy will help you understand the significance of this.
You know that
because there are 12 things in 4 groups of 3. If you didn't know the product
you could find it in several ways. You could lay out 4 groups of 3 things and count them one by one, for example. Or you could use the associative property of multiplication, which means that to find
you can either multiply a and b first, or you can multiply b and c first — the final product is the same either way. Using the associative property, you could think of
is twice as much as
Finally, you could think
That is, one way to compute products is by using repeated addition.
It's the same with exponents:
From 4 and 3, you compute a third number, 64. Just as you can compute
by using repeated addition, you can compute
using repeated multiplication:
But there are other ways too, and these ways depend on properties of exponentiation as an operation. You can double
to get
using the associative property of multiplication, and properties of exponentiation allow you to relate
These properties are known as rules for operating with exponents.
Three major rules appear in eighth grade. In the following statements, A is presumed to be a positive number:
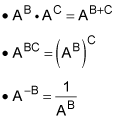
You can understand these rules better by way of examples. You can see the first rule, that
by thinking of
Six threes are multiplied. The second rule you can see by thinking about
Eight threes are multiplied together. The third rule is the logical consequence of the first rule, and of the fact that
when A is any positive number. Here's why:
by the first rule. Then
has to be the reciprocal of
Each of these rules is useful going in both directions. You don't have to view these equations as machines that transform the left-hand side into the right-hand side. Instead, each side of each equation has the same value as the other side. Sometimes you have something that looks like this:
and it's useful to write it as
Sometimes it goes the other way around. What matters is the equivalence — or sameness — of both sides of each equation.

