Being able to identify and generate equivalent fractions is a tremendously important skill in Common Core arithmetic and algebra alike. Fourth graders use pictures and reasoning to write equivalent fractions.
Equivalent fractions are any two fractions that represent the same quantity, as in
and
You may remember spending lots of time reducing fractions, and even getting test questions wrong because you didn't reduce your fractions, but there is absolutely no reason to insist on reduced fractions. A simpler version of a fraction is helpful sometimes. For example, you may not know exactly how much
of an hour is, but you can probably work very easily with its simpler form,
In that sense,
may be a more useful form of the fraction than
but it isn't a more correct form. These two fractions mean the same thing.
Overemphasizing reducing fractions — which is the common term for writing an equivalent fraction using the smallest possible whole numbers for numerator and denominator — has set many students up with misconceptions and needless fear of fractions. The term reduce is a problem, for example, because it suggests that the reduced fraction is smaller than the original one, which isn't true. Similarly, telling students that they're wrong when they write
instead of
leads some students to think that fractions are transformed by the process of reducing — that
and
are somehow different from each other. In fact, they're the same; they're equivalent. In many classrooms, the term simplify replaces reduce to avoid these problems. Simplify suggests that the fraction is in a simpler form — using smaller whole numbers in the numerator and denominator — but that it's the same fraction.
Students may generate equivalent fractions by drawing pictures, as in the following example.
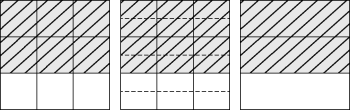
If you start with the fraction
(shown on the left-hand side of the figure), you can show that
covers the same amount of area as
by cutting each of the ninths into two same-sized pieces (in the middle of the figure). You have twice as many pieces in the whole (18 instead of 9), and you have twice as many pieces shaded (12 instead of 6).
Conversely, you can glue ninths together in sets of three to make thirds. When you do, you divide the total number of pieces by three, and you also divide the number of shaded pieces by three, so
as the right-hand side of the figure shows. Your child's teacher or textbook may refer to these pictures as area models, because you pay attention to the fraction of the area of the square (or rectangle, or circle, or whatever) that is shaded.
The next figure shows this same process using a number line.
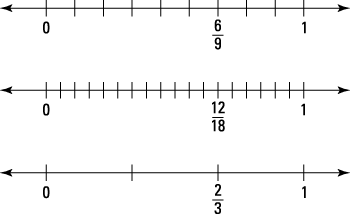
Instead of shading, you keep track of the number of same‐sized pieces between the fraction and zero. The top number line shows
The middle number line shows the result of cutting each ninth in two equal pieces to get
The bottom number line shows the result of grouping the ninths to get






