When performing algebraic distribution, you get the same answer whether you distribute first or add what’s within the parentheses first. Deciding to distribute or add is a judgment call, based on the following conditions:
Distributing first to get the answer is the better choice when the multiplication of each term gives you nicer numbers. Fractions or decimals in the parentheses are sometimes changed into nice whole numbers when the distribution is done first.
Adding up what’s in the parentheses first is preferred when distributing first gives you too many big multiplication problems.
Sometimes it’s easy to tell which case you have. At other times, you just have to guess and try it.
These examples show the difference between adding first and distributing first, so that you can see when each operation offers an advantage.
Example 1: Distribute 60 over 1/2 + 3/5 – 3/4 + 13/15.
If you add first: Find a common denominator and then add and subtract the fractions.
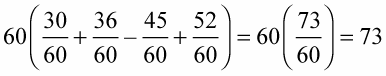
If you distribute first: Multiply each term by 60.
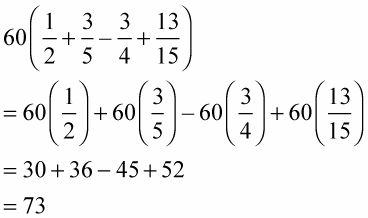
As this example shows, multiplying by 60 gets rid of all the fractions, so you don’t have to find a common denominator, making distributing first much easier. When a problem begins with fractions or decimals, it's often best to add first.
Example 2: Distribute 43 over 160 – 159 + 433 – 432.
If you add first: Add and subtract the terms in parentheses and then multiply by 43.
43(160 – 159 + 433 – 432) = 43(1 + 1) = 43(2) = 86
If you distribute first: Multiply each term by 43.
43(160 – 159 + 433 – 432) =
43(160) – 43(159) + 43(433) - 43(432) =
6,880 - 6,837 + 18,619 - 18,576 =
86
As this example shows, distributing first results in large numbers that are more difficult to manage when doing addition and subtraction, while adding first makes the problem much easier. When a problem begins with large numbers, it's often best to add first.





