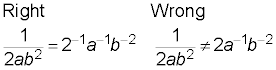The sheer number of people who use algebra means that a large number of errors are unavoidable. So much algebra is done in the world: Just about everyone who advances beyond elementary school takes an algebra class. Forgetting some of the more obscure rules or confusing one rule with another is easy to do when you’re in the heat of the battle with an algebra problem.
But some errors occur because that error seems to be an easier way to do the problem. Not right, but easier — the path of least resistance. These errors usually occur when a rule isn’t the same as your natural inclination. Most algebra rules seem to make sense, so they aren’t hard to remember. Some, though, go against the grain.
The main errors in algebra occur while performing expanding-type operations: distributing, squaring binomials, breaking up fractions, or raising to powers. The other big error area is in dealing with negatives. Watch out for those negative vibes.
Keeping track of the middle term
A squared binomial has three terms in the answer. The term that often gets left out is the middle term: the part you get when multiplying the two outer terms together and the two inner terms together and finding their sum. The error occurs when just the first and last separate terms are squared, and the middle term is just forgotten.
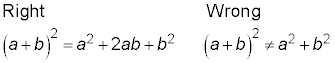
Distributing
Distributing a number or a negative sign over two or more terms in parentheses can cause problems if you forget to distribute the outside value over every single term in the parentheses. The errors come in when you stop multiplying the terms in the parentheses before you get to the end.
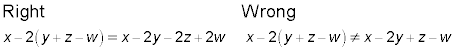
Breaking up fractions
Splitting a fraction into several smaller pieces is all right as long as each piece has a term from the numerator (top) and the entire denominator (bottom). You can’t split up the denominator.
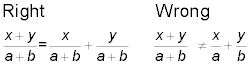
Renovating radicals
If the expression under a radical has values multiplied together or divided, then the radical can be split up into radicals that multiply or divide. You can’t split up addition or subtraction, however, under a radical.
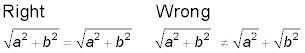
Note: The radical expression is unchanged because the sum has to be performed before applying the radical operation.
Keeping order with operations
The order of operations instructs you to raise the expression to a power before you add or subtract. A negative in front of a term acts the same as subtracting, so the subtracting has to be done last. If you want the negative raised to the power, too, then include it in parentheses with the rest of the value.
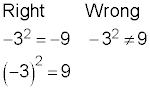
Fracturing fractional exponents
A fractional exponent has the power on the top of the fraction and the root on the bottom.
When writing
as a term with a fractional exponent,
A fractional exponent indicates that there’s a radical involved in the expression. The 2 in the fractional exponent is on the bottom — the root always is the bottom number.
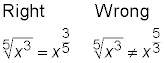
Multiplying bases together
When you’re multiplying numbers with exponents, and those numbers have the same base, you add the exponents and leave the base as it is. The bases never get multiplied together.
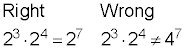
Raising a power to a power
To raise a value that has a power (exponent) to another power, multiply the exponents to raise the whole term to a new power. Don’t raise the exponent itself to a power — it’s the base that’s being raised, not the exponent.
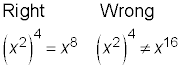
Reducing for a better fit
When reducing fractions with a numerator that has more than one term separated by addition or subtraction, then whatever you’re reducing the fraction by has to divide every single term evenly in both the numerator and the denominator.
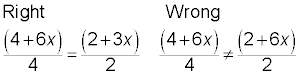
Negating negative exponents
When changing fractions to equivalent expressions with negative exponents, give every single factor in the denominator a negative exponent.