The problem with fractions in linear algebraic equations is that they aren't particularly easy to deal with. For example, they always require common denominators before you can add or subtract them.
The best way to deal with linear equations that involve variables tangled up with fractions is to get rid of the fractions. Your game plan is to multiply both sides of the equation by the least common denominator (also known as the least common multiple) of all the fractions in the equation.
For example, to solve
your first step is to find the least common denominator for these fractions. In this case, the denominators are 5, 7, and 2, which means the least common denominator is 70. Now you multiply each term in the equation by the least common denominator:
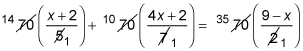
You then distribute the reduced numbers over each parenthesis, combine the like terms, and solve for x:

Keep in mind that extraneous (false) solutions can occur when you alter the original format of an equation. When working with fractions and changing the form of an equation to a more easily solved form, always check your answer in the original equation. For this example, you just insert x = 3 into
and get 1 + 2 = 3 or 3 = 3. This one checks.





