When you need to simplify an algebraic equation that involves logarithms, one way to make the equation much nicer is by using the basic exponential/logarithmic equivalence
If you're asked to evaluate log9 3, for example (or if you have to change it into another form), you can write it as an equation, log9 3 = x, and use the equivalence: 9x = 3. Now you have it in a form that you can solve for x (the x that you get is the answer or value of the original expression). You solve by changing the 9 to a power of 3 and then finding x in the new, more familiar form:
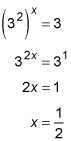
The result tells you that
which is much simpler than the original log expression.
Now look at the process of determining that 10log3 27 is equal to 30. You have to admit that the number 30 is much easier to understand and deal with than 10log3 27, so here are the steps:
Replace log3 27 with x to get 10(log3 27) = 10(x).
Simplify log3 27 by first writing 27 as a power of 3.
27 = 33, so log3 27 = log3 33.
Use the laws of logarithms involving log of a power and log of a base.
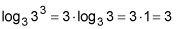
So if x = 3, then 10(x) = 10(3) = 30 or 10log3 27 = 30.
As you can see from the preceding equivalence example, the properties of log functions allow you to do simplifications that you just can't do with other types of functions. For example, because logb b = 1, you can replace log3 3 with the number 1.
Using the rules for the log of 1, the log of the base, the log of a power, and the log of a quotient, you can change a complicated log expression into something equal to –2, for example:


