You can use prime factorization to reduce fractions. Start with numbers only and then add variables (letters that represent any real number) to the mix. The beauty of using the prime factorization method is that you can be sure that the fraction’s reduction possibilities are exhausted — that is, you can be certain that you haven’t missed any factors that the numerator and denominator may have in common.
Example: Use these steps to reduce the following fraction.
Find the prime factorization of the numerator.

Find the prime factorization of the denominator.
165 = 3 × 5 × 11
Write the fraction with the prime factorizations in it.

Cross out the factors the numerator shares with the denominator to see what’s left — the reduced form.

Example: Reduce the following fraction.
Find the prime factorization of the numerator.

Find the prime factorization of the denominator.

Write the fraction with the prime factorizations.

Look at the prime factorizations. You can see that the numerator and denominator have nothing in common. The fraction can’t be reduced, and so the two numbers are relatively prime. The beauty of using prime factorization is that you can be sure that the fraction’s reduction possibilities are exhausted — you haven’t missed anything. You can leave the fraction in this factored form or go back to the simpler 100/243. It depends on your preference.
Example: Reduce the following fraction that includes variables.
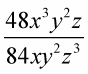
Find the prime factorization of the numerator.
Find the prime factorization of the denominator.

Write the fraction with the prime factorization.

Cross out the factors in common.






