You can identify a quadratic expression (or second-degree expression) because it's an expression that has a variable that's squared and no variables with powers higher than 2 in any of the terms.
Where a is not equal to 0, you can recognize standard quadratic expressions because they follow the form
Part of recognizing a quadratic expression also means being able to write in the standard form to make it easier to work with.
You may notice that the following examples of quadratic expressions each have a variable raised to the second degree. (There’s no power higher than two in any of them):
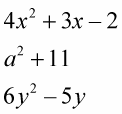
The following lists some properties of standard quadratic expressions to keep in mind so that you can identify them easily:
These expressions are usually written in terms of an x, y, z, or w. The letters at the end of the alphabet are used more frequently for the variable, while those at the beginning of the alphabet are usually used for a number or constant. This doesn’t have to be the case, but it is usually the case.
In a quadratic expression, the a (the variable raised to the second power) can’t be zero. If a were allowed to be 0, then the x to the power of 2 would be multiplied by zero. It wouldn’t be a quadratic expression anymore. The variables b or c can be 0, but a cannot.
Quadratics don’t necessarily have all positive terms, either. The standard form,
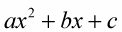
is written with all positives for convenience. But if a, b, or c represented a negative number, then that term would be negative.
The terms are usually written with the second-degree term first, the first-degree next, and the number last.
Give your brain a workout. Change the following into a standard quadratic expression:
Decide which variable makes it a quadratic expression.
Look for the variable that is squared. This can be a second-degree expression in y.
Write the expression in terms of that variable.
After you find the variable that’s squared, write the rest of the expression in decreasing powers of that variable.
Written in the standard form for quadratics,
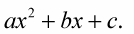
where the second-degree term comes first, it looks like this:
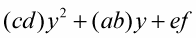
The parentheses aren’t necessary in this case and don’t change anything, but they’re used sometimes for emphasis. The parentheses just make seeing the different parts easier.

