Well, it doesn’t mean x times zero, so the answer isn’t zero. x represents some unknown real number; it just can’t be zero. To understand how this works, use the following rule for division of exponential expressions involving zero.
Any number to the power of zero equals one, as long as the base number is not zero.
For example, to divide
use the rule for dividing exponential expressions, which says that if the base is the same, subtract the two exponents in the order that they’re given. Doing this, you find that the answer is
This is true of all numbers that can be written as a division problem, which means that it’s true for all numbers except those with a base of zero.
See how this power of zero works:
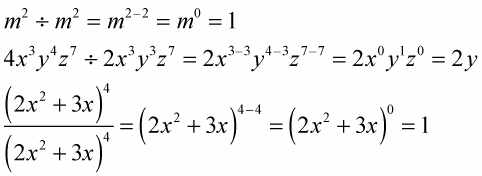
Notice that the x and z, each with their zero exponents, then become ones. And when you multiply by 1, the value is unchanged.

