Sets of elements can be combined or changed by using set operations. Much like addition or subtraction of real numbers, set operations are strictly defined to do something to the sets involved. The set operations are union, intersection, and complement:
The union of two sets A and B asks for all the elements in sets A and B — all of them together (without repeating any elements that they share).
The intersection of the two sets A and B asks for all the elements that A and B have in common. If the two sets have nothing in common, then your answer is the empty set or null set.
The complement of a set A asks for all the elements that aren’t in the set but are in the universal set. The universal set is everything under consideration at the time. For instance, if you’re working on sets that contain the letters of the English alphabet, then the universal set is all 26 letters.
Sample questions
Given the sets A = {2, 4, 6, 8}, B = {4, 8, 16, 24, 32}, C = {3, 6, 9, 12, 15, 18, 21}, and the universal set is

The union of A and B consists of all the elements in A and B both, so

Notice that the 4 and 8 aren’t repeated. The intersection of A and B consists of all the elements the two sets share, so

The intersection of B and C is all the elements that the two sets share, but the two sets have nothing in common, so
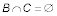
The complement of set C consists of everything that’s in the universal set that’s not in set C, so

Given the sets D = {0, 1, 2, 3, 4}, E = {0, 2, 6, 10}, F = {1, 3, 6, 10}, and U = {0, 1, 2, 3, … , 10}, find the sets


The parentheses in these set operation problems work the same way as parentheses in algebraic expressions — you perform what’s inside the parentheses first. To find the complement of the intersection of sets D and F, you first find the intersection D and F = {1, 3}; then, referring back to the universal set, U, you find the complement:
The complement is everything except the 1 and 3 in the intersection. To find the intersection of the two unions, first find the two unions: the union of D and E = {0, 1, 2, 3, 4, 6, 10}, and the union of E and F = {0, 1, 2, 3, 6, 10}. You write the intersection — what the two results have in common — as
Practice questions
1.Given the sets A = {0, 2, 4, 6, 8, … , 20}, B = {0, 5, 10, 15, 20}, C = {7, 11, 17}, and the universal set U = {0, 1, 2, 3, 4, … , 20}, find the intersection ofA and B.
2.Given the sets A = {0, 2, 4, 6, 8, … , 20}, B = {0, 5, 10, 15, 20}, C = {7, 11, 17}, and the universal set U = {0, 1, 2, 3, 4, … , 20}, find the union of A and B.
Following are answers to the practice questions:
The answer is {0, 10, 20}.
The sets A and B share only these three elements.
The answer is {0, 2, 4, 5, 6, 8, 10, 12, 14, 15, 16, 18, 20}.
The union of A and B contains everything from A — all the even numbers from 0 to 20 — and everything from B — the multiples of 5 from 0 to 20. Essentially, you just list the even numbers and insert the 5 and 15 from set B. The 0 and 10 and 20 are already accounted for.





