The composition of functions is an algebraic operation in which you use one function as the input into another and perform the operations on that input function.
You can perform the basic mathematical operations of addition, subtraction, multiplication, and division on the equations used to describe functions. ( You can also perform whatever simplification is possible on the different parts of the expression and write the result as a new function.)
For example, you can take the two functions f (x) = x2 – 3x – 4 and g(x) = x + 1 and perform the four operations on them:
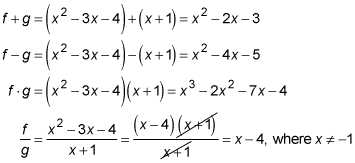
You can use any of these functions to perform a composition.
You indicate the composition of functions f and g with a small circle between the function names,
and you define the composition as
Here's how you perform an example composition, using the functions f and g, f (x) = x2 – 3x – 4 and g(x) = x + 1:
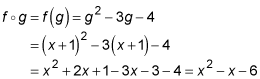
The composition of functions isn't commutative (addition and multiplication are commutative, because you can switch the order and not change the result). The order in which you perform the composition — which function comes first — matters. The composition
isn't the same as
save one exception: when the two functions are inverses of one another.





