When working with big data statistics, you identify the spread of a dataset from the center with several different summary measures: variance, standard deviation, quartiles, interquartile range (IQR).
Variance is the average squared deviation between the elements of the dataset and the mean. For a sample of data, the variance is computed like this:
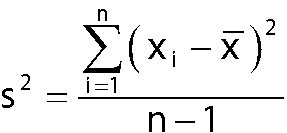
where
xi is the value of a single element in the sample.
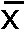
is the sample mean.
n is the sample size.
The standard deviation is the square root of the variance. For most applications, the standard deviation is more convenient to use than the variance as a measure of spread. That's because variance is measured in squared units, whereas standard deviation is measured in the same units as the data. For example, the variance of a dataset consisting of prices would be measured in dollars squared, and the standard deviation would be measured in dollars. Standard deviation is the most widely used measure of the spread in a dataset.
Quartiles divide a dataset into four equal parts. The first quartile (Q1) divides the data into the lowest 25 percent of the observations and the highest 75 percent (25 percent of the observations are less than Q1, and 75 percent are greater than Q1). The second quartile (Q2) divides the data into the lowest 50 percent of the observations and the highest 50 percent. The third quartile (Q3) divides the data into the lowest 75 percent of the observations and the highest 25 percent. The interquartile range (IQR) equals the difference between the third and first quartiles:
The IQR represents the middle 50 percent of the data.
The quartiles of a dataset are best illustrated with a box plot. The following figure shows a box plot of the daily returns to ExxonMobil in 2013.
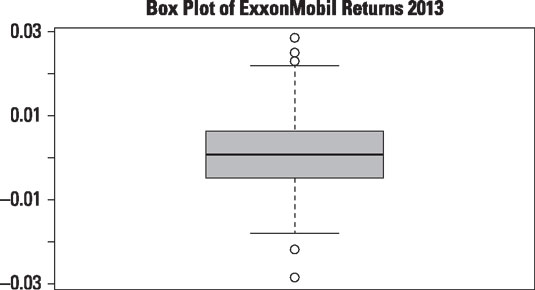
The box plot shows several key statistics for the ExxonMobil returns:
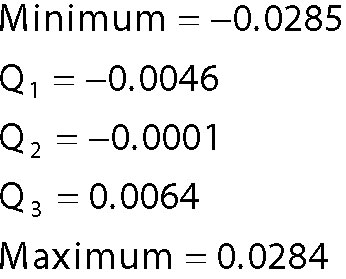
The minimum return is shown on a graph as a single point at the bottom of the plot (a box plot shows outliers as individual points). Q1 is shown as the bottom of the box, Q2 is the solid black line in the middle of the box, and Q3 is the top of the box. The maximum return is shown as a single point at the top of the plot.

