There are several Exploratory Data Analysis (EDA) techniques you can use to test assumptions about a dataset. These include run sequence plot, lag plot, histogram, and normal probability plot.
Run sequence plot
Many statistical techniques are based on the assumption that the data being analyzed has the following properties:
Independent variables
Variables drawn from a common probability distribution
Variables with common parameters (for example, mean and standard deviation)
A run sequence plot tests whether the data conforms to these assumptions. For example, the following figure shows a run sequence plot for the daily returns to the Standard and Poor's stock market index.
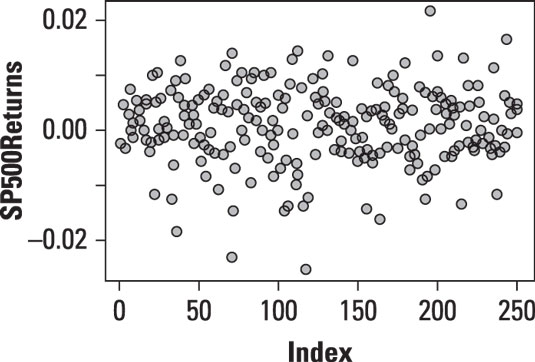
Because this is a time series plot, it's being used to determine whether the returns to the S&P 500 are independent of each other, whether they are all drawn from the same probability distribution, and whether the parameters (mean and variance) remain constant over time.
The run sequence plot is designed to answer these questions:
Are there any changes in the mean of the data?
Are there any changes in the variance of the data?
In addition, you use the run sequence plot to identify any outliers in the data.
The plot of the returns to the S&P 500 shows that the mean and variance of the data remain stable over time, and that there do not appear to be any outliers.
Lag plot
A lag plot determines whether the elements of a dataset are random (independent of each other). In other words, the plot shows whether or not there's a pattern in the data. Patterns in the data are inconsistent with randomness.
A lagged value is one that has occurred in the past. A lag of 1 refers to an observation that has taken place one period in the past. A lag of 2 refers to an observation that has taken place two periods in the past, and so forth.
A lag plot shows the values of a variable on the vertical axis, and the lagged values of the same variable on the horizontal axis. For example, this figure shows a lag plot for the daily returns to the Standard and Poor's stock market index.
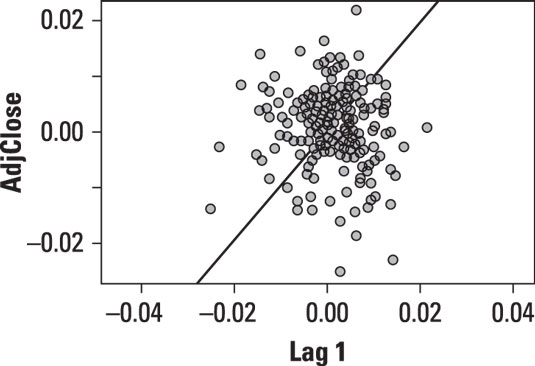
The points on this plot are randomly scattered with no particular pattern. This is consistent with the assumption of randomness in the data.
Histogram
You can use a histogram to identify the distribution followed by a dataset. A histogram can show several key details about a dataset, including the following:
The center of the data
The spread (variability) of the data
The skewness of the data (if any)
The presence of outliers
For example, this figure shows a histogram for the daily returns to the Standard and Poor's stock market index.
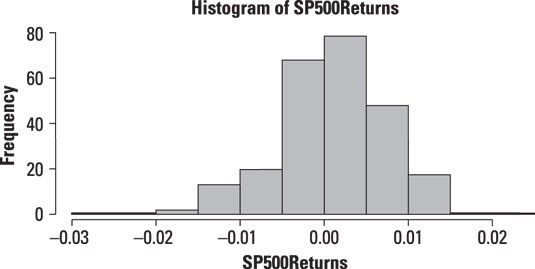
The graph shows that the Standard and Poor's returns have a mean of approximately 0 — the heights of the bars are greatest near 0. The returns appear to exhibit negative skewness (that is, extreme negative returns are more common than extreme positive returns) and have a greater magnitude. There do not appear to be any outliers in the data.
Normal probability plot
Use a normal probability plot to compare a dataset to the normal distribution. The vertical axis of this plot shows the quantiles of the dataset, and the horizontal axis shows the quantiles of the normal distribution. If a dataset is normally distributed, then the graph should appear to be a straight line with a slope of 1.
Quantiles are used to divide a dataset into equally sized groups. A widely used type of quantile is the quartile, which (as discussed earlier) divides a dataset into four equal groups, each consisting of 25 percent of the data. Another popular choice is the percentile, which divides a dataset into one hundred equal groups, each consisting of 1 percent of the data.
The following figure shows a normal probability plot for the daily returns to the Standard and Poor's stock market index.
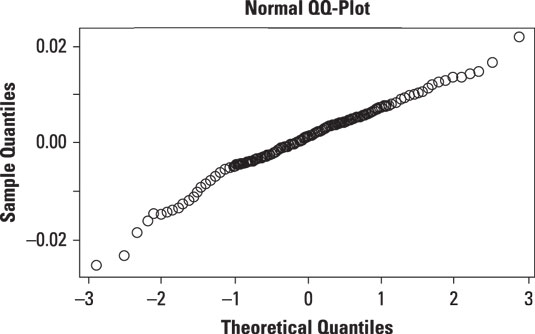
The plot shows that the returns to the S&P 500 are close to being normal, with deviations in the tails of the distribution.

