If you use a large enough statistical sample size, you can apply the Central Limit Theorem (CLT) to a sample proportion for categorical data to find its sampling distribution. The population proportion, p, is the proportion of individuals in the population who have a certain characteristic of interest (for example, the proportion of all Americans who are registered voters, or the proportion of all teenagers who own cellphones). The sample proportion, denoted
(pronounced p-hat), is the proportion of individuals in the sample who have that particular characteristic; in other words, the number of individuals in the sample who have that characteristic of interest divided by the total sample size (n).
For example, if you take a sample of 100 teens and find 60 of them own cellphones, the sample proportion of cellphone-owning teens is
The sampling distribution of
has the following properties:
Its mean, denoted by
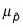
(pronounced mu sub-p-hat), equals the population proportion, p.
Its standard error, denoted by
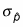
(say sigma sub-p-hat), equals:
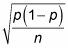
(Note that because n is in the denominator, the standard error decreases as n increases.)
Due to the CLT, its shape is approximately normal, provided that the sample size is large enough. Therefore you can use the normal distribution to find approximate probabilities for
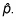
The larger the sample size (n) or the closer p is to 0.50, the closer the distribution of the sample proportion is to a normal distribution.
If you are interested in the number (rather than the proportion) of individuals in your sample with the characteristic of interest, you use the binomial distribution to find probabilities for your results.
How large is large enough for the CLT to work for sample proportions? Most statisticians agree that both np and n(1 – p) should be greater than or equal to 10. That is, the average number of successes (np) and the average number of failures n(1 – p) needs to be at least 10.
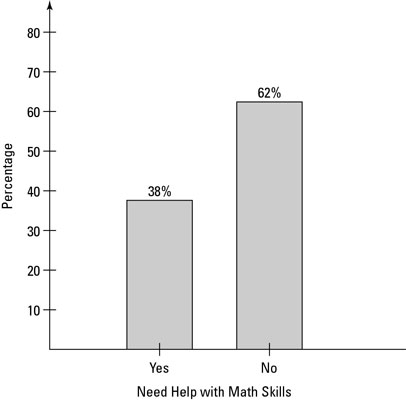
To help illustrate the sampling distribution of the sample proportion, consider a student survey that accompanies the ACT test each year asking whether the student would like some help with math skills. Assume (through past research) that 38% of all the students taking the ACT respond yes. That means p, the population proportion, equals 0.38 in this case. The distribution of responses (yes, no) for this population are shown in the above figure as a bar graph.
Because 38% applies to all students taking the exam, you can use p to denote the population proportion, rather than
which denotes sample proportions. Typically p is unknown, but this example gives it a value to point out how the sample proportions from samples taken from the population behave in relation to the population proportion.
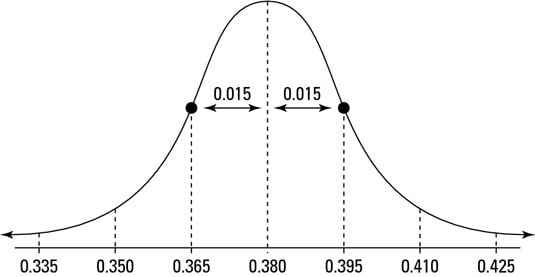
Now take all possible samples of n = 1,000 students from this population and find the proportion in each sample who said they need math help. The distribution of these sample proportions is shown in the above figure. It has an approximate normal distribution with mean p = 0.38 and standard error equal to:
(or about 1.5%).
The approximate normal distribution works because the two conditions for the CLT are met:
And because n is so large (1,000), the approximation is excellent.

