Pre-Calculus: 1001 Practice Problems For Dummies (+ Free Online Practice)
Explore Book Buy On AmazonYou’ll work on graphing complex numbers. Polar coordinates are quite different from the usual (x, y) points on the Cartesian coordinate system. Polar coordinates bring together both angle measures and distances, all in one neat package. With the polar coordinate system, you can graph curves that resemble flowers and hearts and other elegant shapes.
You’ll work on complex numbers and polar coordinates in the following ways:
Interpreting graphs of basic polar coordinates
Graphing polar equations such as cardioids and lemniscates
When working with complex numbers and polar coordinates, some challenges will include the following:
Moving in a counterclockwise direction when graphing polar coordinates
Recognizing which ray to use when graphing negative and multiple angle measures
Practice problems
Identify the point on the polar coordinate plane. Give your answer in
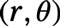
form, where
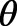
is in radians.
![[Credit: Illustration by Thomson Digital]](https://www.dummies.com/wp-content/uploads/455322.image2.jpg) Credit: Illustration by Thomson Digital
Credit: Illustration by Thomson DigitalAnswer: i301
The point is on the 2-unit ring, so the radius is 2. You measure the angle from the positive x-axis in a counterclockwise direction. Each ray represents 15 degrees, so this point is on the ray representing
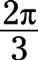
The radius is 2, so the point is 2 units out from the origin.
Change the polar coordinates to rectangular coordinates.
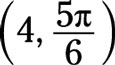
Answer:
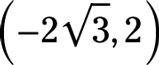
You find the x coordinate with
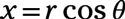
so
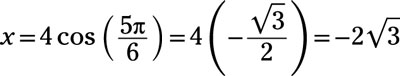
You find the y coordinate with
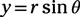
so