Next, multiply 5 by 7. This time, 5 x 7 = 35. But you also need to add the 2 that you carried over, which makes the result 37. Because 5 and 7 are the last numbers to multiply, you don't have to carry, so write down the 37 — you find that 53 x 7 = 371:
When multiplying larger numbers, the idea is similar. For example, suppose you want to multiply 53 by 47. Be sure to align the stacked numbers by the ones place. (The first few steps — multiplying by the 7 in 47 — are the same, so pick up the next step.) Now you're ready to multiply by the 4 in 47. But remember that this 4 is in the tens column, so it really means 40. So to begin, put a 0 directly under the 1 in 371:
This 0 acts as a placeholder so that this row is aligned properly.
When multiplying by larger numbers with two digits or more, use one placeholding zero when multiplying by the tens digit, two placeholding zeros when multiplying by the hundreds digit, three zeros when multiplying by the thousands digit, and so forth.
Now you multiply 3 x 4 to get 12, so write down the 2 and carry the 1:Continuing, multiply 5 x 4 to get 20, and then add the 1 that you carried over, giving a result of 21:
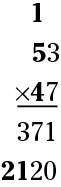
To finish, add the two products (the multiplication results):
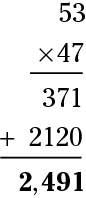
So 53 x 47 = 2,491.

