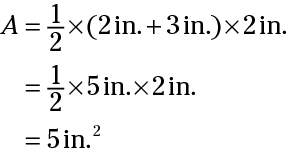Measuring squares
The letter s represents the length of a square's side. For example, if the side of a square is 3 inches, then you say s = 3 in. Finding the perimeter (P) of a square is simple: Just multiply the length of the side by 4. Here's the formula for the perimeter of a square:For example, if the length of the side is 3 inches, substitute 3 inches for s in the formula:
Finding the area of a square is also easy: Just multiply the length of the side by itself — that is, take the square of the side. Here are two ways of writing the formula for the area of a square (s2 is pronounced "s squared"):
For example, if the length of the side is 3 inches, then you get the following:
Working with rectangles
The long side of a rectangle is called the length, or l for short. The short side is called the width, or w for short. For example, in a rectangle whose sides are 5 and 4 feet long, l = 5 ft. and w = 4 ft.Because a rectangle has two lengths and two widths, you can use the following formula for the perimeter of a rectangle:
Calculate the perimeter of a rectangle whose length is 5 yards and whose width is 4 yards as follows:
The formula for the area of a rectangle is:
So here's how you calculate the area of the same rectangle:
Calculating with rhombuses
As with a square, use s to represent the length of a rhombus's side. But another key measurement for a rhombus is its height. The height of a rhombus (h for short) is the shortest distance from one side to the opposite side. Here, s = 4 cm and h = 2 cm.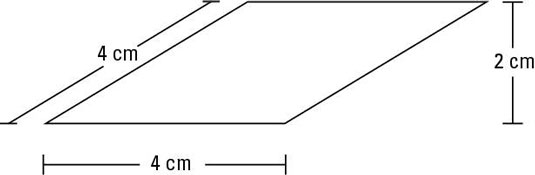
The formula for the perimeter of a rhombus is the same as for a square:
Here's how you figure out the perimeter of a rhombus whose side is 4 centimeters:
To measure the area of a rhombus, you need both the length of the side and the height. Here's the formula:
So here's how you determine the area of a rhombus with a side of 4 cm and a height of 2 cm:
You can read 8 cm2 as "8 square centimeters" or, less commonly, as "8 centimeters squared."
Measuring parallelograms
The top and bottom sides of a parallelogram are called its bases (b for short), and the remaining two sides are its sides (s). And as with rhombuses, another important measurement of a parallelogram is its height (h), the shortest distance between the bases. So the parallelogram here has these measurements: b = 6 in., s = 3 in., and h = 2 in.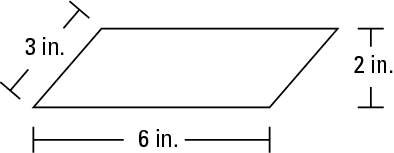
Each parallelogram has two equal bases and two equal sides. Therefore, here's the formula for the perimeter of a parallelogram:
To figure out the perimeter of the parallelogram, just substitute the measurements for the bases and sides:
And here's the formula for the area of a parallelogram:
Here's how you calculate the area of the same parallelogram:
Measuring trapezoids
The parallel sides of a trapezoid are called its bases. Because these bases are different lengths, you can call them b1 and b2. The height (h) of a trapezoid is the shortest distance between the bases. Thus, the trapezoid here has these measurements: b1 = 2 in., b2 = 3 in., and h = 2 in.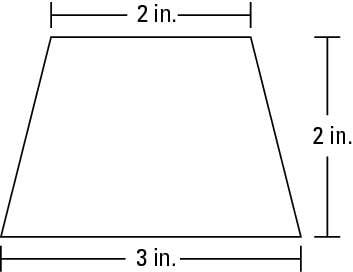
Because a trapezoid can have sides of four different lengths, you really don't have a special formula for finding the perimeter of a trapezoid. Just add up the lengths of its sides, and you get your answer.
Here's the formula for the area of a trapezoid:
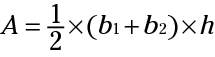
So here's how to find the area of the pictured trapezoid: