In geometry, a dilation is a transformation that changes only the size of a geometric shape, while leaving its shape and orientation unchanged. In the following practice questions, you're asked to calculate the constant of dilation, and then find the dilated image of given coordinates.
The center of dilation is the origin.
Practice questions
If Point
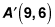
is the image of Point A (3, 2) under a dilation with respect to the origin, what is the constant of dilation?
A dilation maps J (6, 3) to
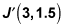
What would the image of K (–2, 10) be under the same dilation?
Answers and explanations
3
A dilation changes the distance between points by multiplying the x and y coordinates by the scale factor. The x coordinate for A is 3, and the x coordinate for
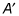
is 9. If you call the scalar factor k, then
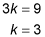
You can also determine the scale factor by looking at the y coordinates. The y coordinate for A is 2, and the y coordinate for
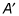
is 6, so
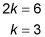
(–1, 5)
A dilation changes the distance between points by multiplying the x and y coordinates by the scale factor. The x coordinate for J is 6, and the x coordinate for
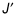
is 3. If you call the scalar factor k, then
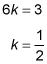
Multiply the coordinates of K by the scale factor of 1/2:
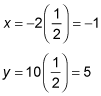
The image is therefore (–1, 5).

