Using exponential expressions to solve problems that involve repeated actions is the best way to find the answer. Exponential expressions help you figure out problems that do the same thing over and over by using powers, or exponents, to make computation easier.
For example, picture a cat stalking a mouse. They’re about 100 inches apart. Every time the mouse starts nibbling at a hunk of cheese, the cat takes advantage of the mouse’s distraction and creeps closer by one-tenth the distance between them. The cat wants to get about 6 inches away — close enough to pounce. How far apart are they after three moves? How about after ten moves? How long will it take before the cat can pounce on the mouse?
An easy way to solve this problem is to find the distance remaining between them after the cat’s first move, which is nine-tenths of the distance before that move. One-tenth plus nine-tenths equals one — the original distance.
In each step, you multiply by 9/10, which is the fraction of the distance left after the move times the current distance. Nine-tenths times the current distance = the new distance. Then there’s just one operation to deal with each time.
Find the distance left between them after the first move by multiplying the current distance by 9/10.
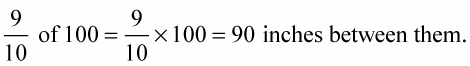
Find the distance left between them after the second move by multiplying the current distance by 9/10.
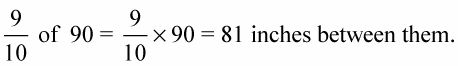
Find the distance left between them after the third move by multiplying the current distance by 9/10.
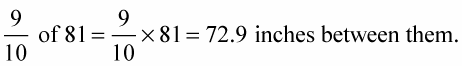
Find the distance left between them after the fourth move by multiplying the current distance by 9/10.
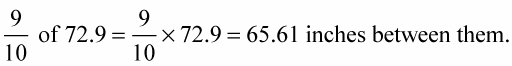
As you see, this can get pretty tedious. The best way to find the answer is to use exponents. Figuring this problem using powers, or exponents, can make the computation easier. Just follow these steps:
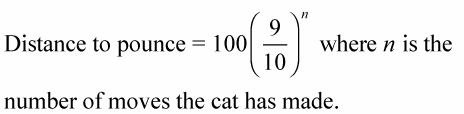
Perform the operations inside the grouping symbol first.
In this formula, because the fraction 9/10 is inside parentheses, apply the exponent just outside the parentheses to the fraction first. Multiply the fraction n times itself before multiplying it by 100.
Find the distance between the cat and the mouse using this formula:

This still isn’t close enough to pounce. The approximately symbol is used here because the actual answer has many more decimal places and you don’t need all that information.
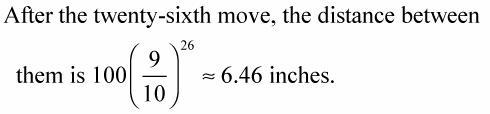
It’ll take one more move to be within the six-inch pounce distance. Do you suppose the mouse still hasn’t caught on after 26 moves? If not, then it deserves to be pounced upon.

