You must find a common denominator if you want to add, subtract, or compare fractions that have different denominators. A common denominator, which means having the same number in the denominator (or the bottom) of each fraction, creates equivalent fractions that can be added, subtracted, or compared.
Finding a common denominator means finding one number that each denominator can divide into easily.
Example: What’s the common denominator for the following expressions?
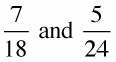
Determine which fraction has the larger denominator.
In this case, 24 is the larger of the two denominators.
Check to see if the smaller denominator divides into the larger one evenly.
18 doesn’t divide into 24 evenly, so you need to move on to the next step.
If the smaller denominator does divide the larger one evenly, you can skip step 3. For instance, if 3 and 9 were the denominators, you would find that 3 divides into 9 evenly — by 3 — and 9 would then be the common denominator!
Check multiples of the larger denominator.
Check multiples of the larger denominator until you find a number that the smaller denominator can also divide into evenly.
2 × 24 = 48, but 18 doesn’t divide 48 evenly.
3 × 24 = 72, and 18 does divide that evenly. So, the common denominator in this example is 72.
Write the first fraction as an equivalent fraction with the common denominator.
18 divides into 72 four times, so the fraction 7/18 is multiplied by 4/4:
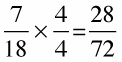
Write the second fraction as an equivalent fraction with the common denominator.
24 divides into 72 three times, so the fraction 5/24 is multiplied by 3/3:
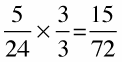
So with the common denominator of 72:
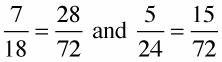
You can now easily add, subtract, or compare the two fractions!

