A piecewise function consists of two or more function rules (function equations) pieced together (listed separately for different x values) to form one bigger function.
A change in the function equation occurs for different values in the domain. For example, you may have one rule for all the negative numbers, another rule for numbers bigger than three, and a third rule for all the numbers between those two rules.
Piecewise functions have their place in situations where you don't want to use the same rule for everyone or everything. Should a restaurant charge a 3-year-old the same amount for a meal as it does an adult? Do you put on the same amount of clothing when the temperature is 20 degrees as you do in hotter weather? No, you place different rules on different situations. In mathematics, the piecewise function allows for different rules to apply to different numbers in the domain of a function.
The following is an example of a piecewise function:
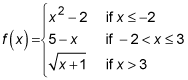
With this function, you use one rule for all numbers smaller than or equal to –2, another rule for numbers between –2 and 3 (including the 3), and a final rule for numbers larger than 3. You still have only one output value for every input value. For instance, say you want to find the values of this function for x equaling –4, –2, –1, 0, 1, 3, and 5. Notice how you use the different rules depending on the input value:
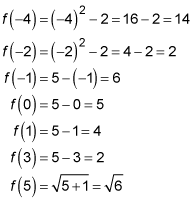
The figure shows you the graph of the piecewise function with these function values.
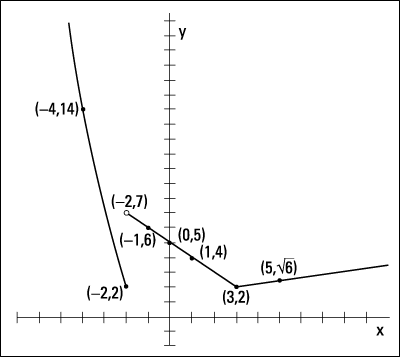
Notice the three different sections to the graph. The left curve and the middle line don't connect because a discontinuity exists when x = –2. A discontinuity occurs when a gap or hole appears in the graph. Also, notice that the left line falling toward the x-axis ends with a solid dot, and the middle section has an open circle just above it. These features preserve the definition of a function — only one output for each input. The dot tells you to use the rule on the left when x = –2.
The middle section connects at point (3, 2) because the rule on the right gets really, really close to the same output value as the rule in the middle when x = 3. Technically, you should draw both a hollow circle and a dot, but you really can't spot this feature just by looking at it.

