How to Find the Second-Order Corrections to Energy Levels and Wave Functions

In quantum physics, in order to find the second-order corrections to energy levels and wave functions of a perturbed system, E_n, you need to calculate E⁽²⁾_n, as well as

So how do you do that? You start with three perturbed equations:

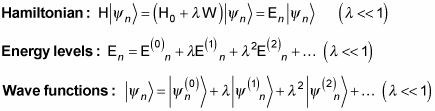
You then combine these three equations to get this jumbo equation:

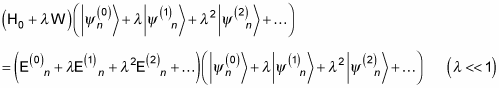
From the jumbo equation, you can then find the second-order corrections to the energy levels and the wave functions. To find E⁽²⁾_n, multiply both sides of

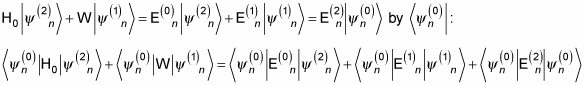
This looks like a tough equation until you realize that

is equal to zero, so you get

Because

is also equal to zero, and again neglecting the first term, you get

E⁽²⁾_n is just a number, so you have

And of course, because

you have

Note that if

is an eigenstate of W, the second-order correction equals zero.

Okay, so

How can you make that simpler? Well, from using

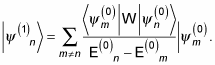
Substituting that equation into

gives you

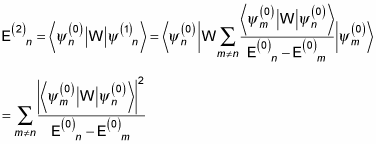
Now you have

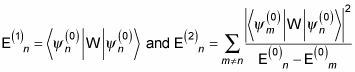
Here's the total energy with the first- and second-order corrections:

So from this equation, you can say

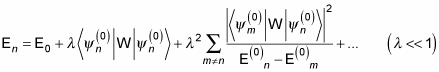
That gives you the first- and second-order corrections to the energy, according to perturbation theory.