You can determine what happens to the wave function when you swap particles in a multi-particle atom. Whether the wave function is symmetric or antisymmetric under such operations gives you insight into whether two particles can occupy the same quantum state.
Given that Pij2 = 1, note that if a wave function is an eigenfunction of Pij, then the possible eigenvalues are 1 and –1. That is, for
an eigenfunction of Pij looks like
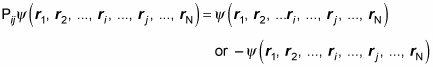
That means there are two kinds of eigenfunctions of the exchange operator:

Now take a look at some symmetric and some antisymmetric eigenfunctions. How about this one — is it symmetric or antisymmetric?
You can apply the exchange operator P12:
Note that because
is a symmetric wave function; that’s because
How about this wave function?
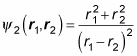
Again, apply the exchange operator, P12:
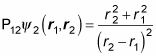
Okay, but because
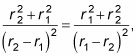
you know that
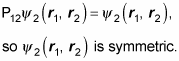
Here’s another one:
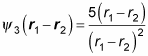
Now apply P12:
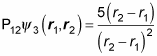
How does that equation compare to the original one? Well,
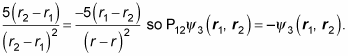
Therefore,
is antisymmetric.
What about this one?
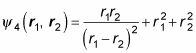
To find out, apply P12:
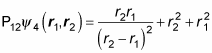
All right — how’s this compare with the original equation?
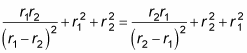
Okay —
is symmetric.
You may think you have this process down pretty well, but what about this next wave function?
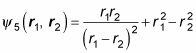
Start by applying P12:
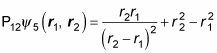
So how do these two equations compare?
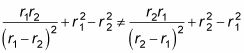
That is,
is neither symmetric nor antisymmetric. In other words,
is not an eigenfunction of the P12 exchange operator.






