Though the principles of quantum electrodynamics were worked out by three individuals, the most famous founder of QED was undeniably Richard P. Feynman. Feynman was equally good at the mathematics and explanation of a theory, which resulted in his creation of Feynman diagrams — a visual representation of the mathematics that went on in QED.
Richard Phillips Feynman is one of the most interesting characters in 20th century physics, easily ranking with Einstein in personality, if not in pure fame. Early on in his career, Feynman made the conscious decision to only work on problems that he found interesting, something that certainly served him well. Fortunately for the world of physics, one of these problems was quantum electrodynamics.
Because electromagnetism is a field theory, the result of QED was a quantum field theory — a quantum theory that contains a value at every point in space. You can imagine that the mathematics of such a theory was intimidating, to say the least, even to those trained in physics and mathematics.
Feynman was brilliant not only with physical theory and mathematics, but also with explanation. One way he simplified things was through the application of his Feynman diagrams. Though the math was still complex, the diagrams meant you could begin talking about the physics without needing all the complexity of the equations. And when you did need the actual numbers, the diagrams helped organize your computations.
In this figure, you can see a Feynman diagram of two electrons approaching each other. The Feynman diagram is set on a Minkowski space, which depicts events in space-time. The electrons are the solid lines (called propagators), and as they get near to each other, a photon (the squiggly propagator) is exchanged between the two electrons.
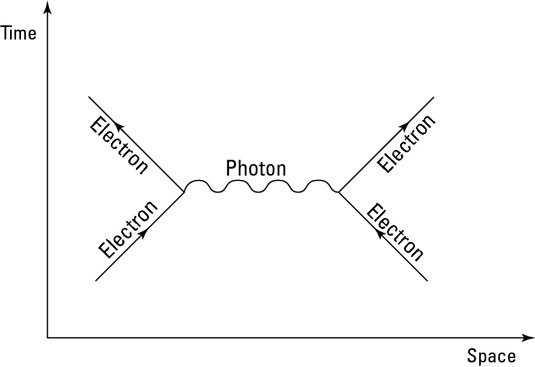
In other words, in QED two particles communicate their electromagnetic information by emitting and absorbing a photon. A photon that acts in this manner is called a virtual photon or a messenger photon, because it’s created solely for the purpose of exchanging this information.
This was the key insight of QED, because without this exchange of a photon, there was no way to explain how the information was communicated between the two electrons.
Also (and perhaps more important from a physics standpoint), a quantum field theory (at least those that seem to match our real world) quickly reaches infinity if distances become too small. To see how these infinities can arise, consider both the fact that electromagnetic forces get larger at small distances (infinitely larger at infinitely small distances) and also the distance and momentum relationship from the uncertainty principle of quantum mechanics.
Even talking about the instances where two electrons are incredibly close to each other (such as within a Planck length) becomes effectively impossible in a world governed by quantum physics.
By quantizing electromagnetics, as QED does, Feynman, Schwinger, and Tomonaga were able to use the theory despite these infinities. The infinities were still present, but because the virtual photon meant that the electrons didn’t need to get so close to each other, there weren’t as many infinities, and the ones that were left didn’t enter physical predictions.
Feynman, Schwinger, and Tomonaga took an infinite theory and extracted finite predictions. One of the major motivations for the drive to develop a successful string theory is to go even further and get an actually finite theory.
The mathematical process of removing infinities is called renormalization. This is a set of mathematical techniques that can be applied to provide a very carefully defined limit for the continuum of values contained in the field.
Instead of adding up all the infinite terms in the calculation and getting an infinite result, physicists have found that applying renormalization allows them to redefine parameters within the summation so it adds up to a finite amount!
Without introducing renormalization, the values become infinite, and we certainly don’t observe these infinities in nature. With renormalization, however, physicists get unambiguous predictions that are among the most precise and best-tested results in all of science.

