In physics, when you break a vector into its parts, those parts are called its components. For example, in the vector (4, 1), the x-axis (horizontal) component is 4, and the y-axis (vertical) component is 1. Typically, a physics problem gives you an angle and a magnitude to define a vector; you have to find the components yourself using a little trigonometry.
Suppose you know that a ball is rolling on a flat table at 15 degrees from a direction parallel to the bottom edge at a speed of 7.0 meters/second. You may want to find out how long the ball will take to roll off the edge 1.0 meter to the right.
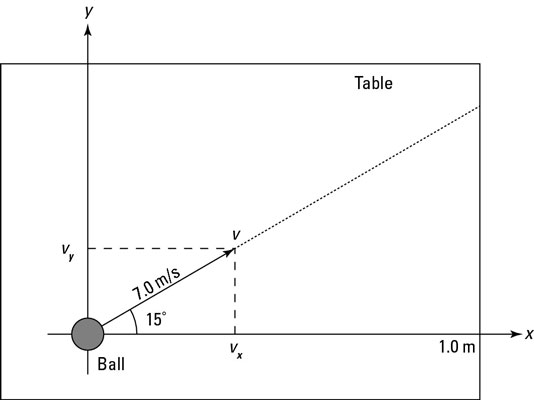
Define your axes so the ball is at the origin initially and the x-axis is parallel to the bottom edge of the table (refer to the figure). Therefore, the problem breaks down to finding out how long the ball will take to roll 1.0 meter in the x direction. To find the time, you first need to know how fast the ball is moving in the x direction.
The problem tells you that the ball is rolling at a speed of 7.0 meters/second at 15 degrees to the horizontal (along the positive x-axis), which is a vector: 7.0 meters/second at 15 degrees gives you both a magnitude and a direction. What you have here is a velocity — the vector version of speed. The ball’s speed is the magnitude of its velocity vector, and when you include a direction to that speed, you get the velocity vector v.
To find out how fast the ball is traveling toward the table edge, you need not the ball’s total speed but the x component of the ball’s velocity. The x component is a scalar (a number, not a vector), and you write it like this: vx. The y component of the ball’s velocity vector is vy. Therefore, you can say that
v = (vx, vy)
That’s how you express breaking a vector up into its components. So what’s vx here? And for that matter, what’s vy, the y component of the velocity? The vector has a length (7.0 meters/second) and a direction
And you know that the edge of the table is 1.0 meter to the right.
As you can see in the figure, you have to use some trigonometry to resolve this vector into its components. No sweat. The trig is easy after you get down the angles you see in the figure.
The magnitude of a vector v is expressed as v, and from the figure, you can see that the following is true:

The two vector-component equations are worth knowing because you see them a lot in any beginning physics course. Make sure you know how they work, and always have them at your fingertips.
Of course, if you forget these equations, you can always retrieve them from basic trigonometry. You may remember that the sine and cosine of an angle in a right triangle are defined as the ratio of the opposite side and the adjacent side to the hypotenuse, like so:
By multiplying both sides of these equations by v, you can express the x and y components of the vector as
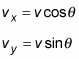
You can go further by relating each side of the triangle to each other side (and if you know that
you can derive all these from the previous two equations as required; no need to memorize all these):
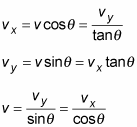
You know that
so you can find the x component of the ball’s velocity, vx, this way:
Plugging in the numbers gives you

You now know that the ball is traveling at 6.8 meters/second to the right. And because you also know that the table’s edge is 1.0 meter away, you can divide distance by speed to get the time:
Because you know how fast the ball is going in the x direction, you now know the answer to the problem: The ball will take 0.15 seconds to fall off the edge of the table. What about the y component of the velocity? That’s easy to find, too:

