You can use the Fundamental Theorem to calculate the area under a function (or just to do any old definite integral) that you integrate with the substitution method. What you want to do is to change the limits of integration and do the whole problem in terms of u. Say you want the area given by
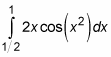
Set u equal to x-squared.
Take the derivative of u with respect to x.

Solve for dx.

Determine the new limits of integration.

Make the substitutions, including the new limits of integration, and cancel the two 2xs.
In this problem, only one of the limits is new because when x = 1, u = 1.

Use the antiderivative and the Fundamental Theorem to get the desired area without making the switch back to x-squared.







