Here are the two standard forms for the equations of parabolas (and what they tell you):
| Equation | Direction the Parabola Opens | Location of the Vertex |
|---|---|---|
| (y – k)2 = 4a(x – h) | Right if a is positive, left if a is negative | (h, k) |
| (x – h)2 = 4a(y – k) | Up if a is positive, down if a is negative | (h, k) |
Sample questions
-
Write the equation of the parabola x2 – 16x – 4y + 52 = 0 in standard form to determine its vertex and in which direction it opens.
(x– 8)2= 4(1)(y+ 3); vertex: (8, –3); opens upward. First rewrite the equation to isolate the x-terms: Leave the two terms with x’s on the left, and get the other two terms on the right by adding 4y and –52 to both sides. You get x2 – 16x = 4y – 52.
Next, complete the square on the left side of the equation. Be sure to add the 64 to both sides of the equation to keep it balanced; x2 – 16x + 64 = 4y – 52 + 64 becomes (x – 8)2 = 4y + 12. Now factor out the 4 from the terms on the right to get (x – 8)2 = 4(y + 3).
The vertex of the parabola is (8, –3). The parabola opens upward, because the x term is squared and the multiplier on the right is positive. The 4a part of the standard form is actually 4(1), if you want to show that the a value is 1.
-
Write the equation of the parabola 2y2 + 28y + x + 97 = 0 in standard form to determine its vertex and in which direction it opens.
(y+ 7)2= (x– 1); vertex: (1, –7); opens left. First, rewrite the equation, leaving the two terms with y’s on the left and moving the others to the right. You get 2y2 + 28y = –x – 97. Factor the 2 out of the terms on the left before completing the square; 2(y2 + 14y) = –x – 97 becomes 2(y2 + 14y + 49) = –x – 97 + 98.
Notice that you have to add 98 to the right, because the 49 that you added to complete the square is multiplied by 2. Simplifying and factoring, you have 2(y + 7)2 = –x + 1. Now factor –1 from each term on the right, and then divide both sides by 2:
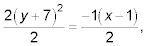
The vertex of the parabola is at (1, –7), and the parabola opens to the left. The coefficient on the right,
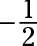
is written
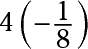
when you want to put it in the 4a form.
Practice questions
-
Write the equation of the parabola x2 – 6x – y + 4 = 0 in standard form to determine its vertex and in which direction it opens.
-
Write the equation of the parabola 2x2 + 8x + y + 3 = 0 in standard form to determine its vertex and in which direction it opens.
-
Write the equation of the parabola 3y2 – 12y – x + 9 = 0 in standard form to determine its vertex and in which direction it opens.
-
The answer is equation: (x– 3)2=y+ 5; vertex: (3, –5); opens upward.
Complete the square on the left by moving the y and 4 to the right side and adding 9 to each side of the equation. Factor and simplify. The parabola opens upward, because the value of 4a, the multiplier on the right, is +1.
-
The answer is equation:
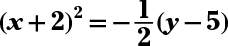
vertex: (–2, 5); opens downward.
Move the y and 3 to the right, and then factor 2 out of the two x terms to get 2(x2 + 4x) = –y + 5. Complete the square in the parentheses, and add 8 to the right side. Simplify and factor to get 2(x + 2)2 = –1(y – 5). Divide each side by 2. The parabola opens downward, because the value of 4a, the multiplier on the right, is
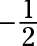
-
The answer is equation:
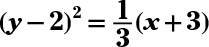
vertex: (–3, 2); opens to the right.
Move the x and 9 to the right. Then factor 3 out of the two y terms to get 3(y2 – 4y) = x – 9. When you complete the square, you have to add 12 on the right. Simplifying and factoring, you get 3(y – 2)2 = x + 3. Divide each side by 3. The parabola opens to the right, because the value of 4a, the multiplier on the right, is positive.

