One way to find the LCM is to list the multiples of each number, one at a time, until you find the smallest multiple that's common to all the numbers.
Try the following example: find the LCM of 45 and 50.
- Multiples of 45: 45, 90, 135, 180, 225, 270, 315, 360, 405, 450
- Multiples of 50: 50, 100, 150, 200, 250, 300, 350, 400, 450
That's rather cumbersome, isn't it? Wouldn't it be great if you had an easier way? Fortunately, you do: An easier way to find the LCM is first to list the prime factors of each number:
- The prime factors for 45 are
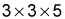
- The prime factors for 50 are
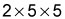
Here's one more example: what is the least common multiple of 5, 27, and 30?
List the prime factors of each number:
- Prime factors of 5: 5
- Prime factors of 27:
- Prime factors of 30:
The number 3 occurs a maximum of three times, 5 occurs a maximum of one time, and 2 occurs a maximum of one time:
Check your answer by seeing whether 5, 27, and 30 can all divide evenly into 270.

