One way to look at superstring theory is to realize that the directions a string can move can only be described with a basis of ten distinct vectors, so the theory describes a 10-dimensional vector space.
One of the major steps of working with vector spaces is to find the basis for the vector space, a way of defining how many vectors you need to define any point in the entire vector space. For example, a 5-dimensional space has a basis of five vectors.
When looking in our world, it has three dimensions — up and down, left and right, back and forth. If you give a longitude, latitude, and an altitude, you can determine any location on Earth, for example.
A straight line in space: Vectors
Expanding on the idea of Cartesian geometry, you find that it’s possible to create a Cartesian grid in three dimensions as well as two, as shown in this figure. In such a grid, you can define an object called a vector, which has both a direction and a length. In 3-dimensional space, every vector is defined by three quantities.
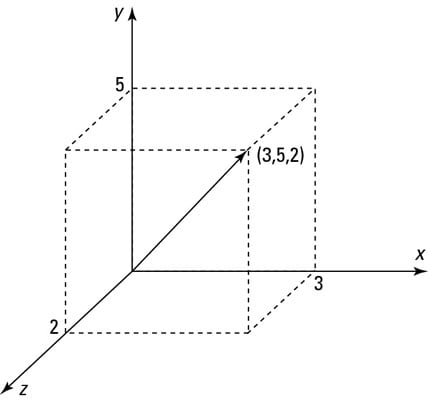
Vectors can, of course, exist in one, two, or more than three dimensions. (Technically, you can even have a zero-dimensional vector, although it will always have zero length and no direction. Mathematicians call such a case “trivial.”)
Treating space as containing a series of straight lines is probably one of the most basic operations that can take place within a space. One early field of mathematics that focuses on the study of vectors is called linear algebra, which allows you to analyze vectors and things called vector spaces of any dimensionality. (More advanced mathematics can cover vectors in more detail and extend into nonlinear situations.)
Twisting 2-dimensional space in three dimensions: The Mobius strip
In the classic book Flatland, the main character is a square (literally — he has four sides of equal length) who gains the ability to experience three dimensions. Having access to three dimensions, you can perform actions on a 2-dimensional surface in ways that seem very counterintuitive. A 2-dimensional surface can actually be twisted in such a way that it has no beginning and no end!
The best known case of this is the Mobius strip, shown in this figure. The Mobius strip was created in 1858 by German mathematicians August Ferdinand Mobius and Johann Benedict Listing.
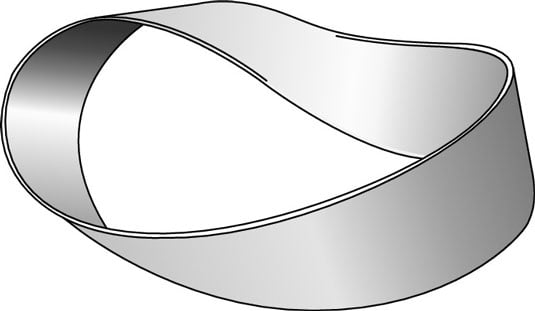
You can create your own Mobius strip by taking a strip of paper — kind of like a long bookmark — and giving it a half-twist. Then take the two ends of the strip of paper and tape them together. Place a pencil in the middle of the surface and draw a line along the length of the strip without taking your pencil off the paper.
A curious thing happens as you continue along. Eventually, without taking your pencil from the paper, the line is drawn on every part of the surface and eventually meets up with itself. There is no “back” of the Mobius strip, which somehow avoids the pencil line. You’ve drawn a line along the entire shape without lifting your pencil.
In mathematical terms (and real ones, given the result of the pencil experiment), the Mobius strip has only one surface. There is no “inside” and “outside” of the Mobius strip, the way there is on a bracelet. Even though the two shapes may look alike, they are mathematically very different entities.
The Mobius strip does, of course, have an end (or boundary) in terms of its width. In 1882, the German mathematician Felix Klein expanded on the Mobius strip idea to create a Klein bottle: a shape that has no inside or outside surface, but also has no boundaries in any direction.
Take a look at this figure to understand the Klein bottle. If you traveled along the “front” of the path (with the x’s), you’d eventually reach the “back” of that path (with the o’s).
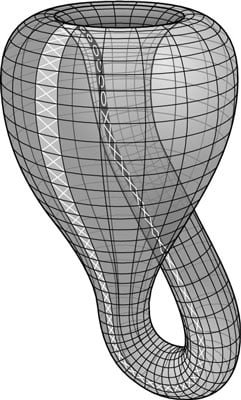
If you were an ant living on a Mobius strip, you could walk its length and eventually get back to where you started. Walking its width, you’d eventually run into the “edge of the world.” An ant living on a Klein bottle, however, could go in any direction and, if it walked long enough, eventually find itself back where it started. (Traveling along the o path eventually leads back to the x’s.)
The difference between walking on a Klein bottle and walking on a sphere is that the ant wouldn’t just walk along the outside of the Klein bottle, like it would on a sphere, but it would cover both surfaces, just like on the Mobius strip.

