The six circle theorems discussed here are all just variations on one basic idea about the interconnectedness of arcs, central angles, and chords (all six are illustrated in the following figure):
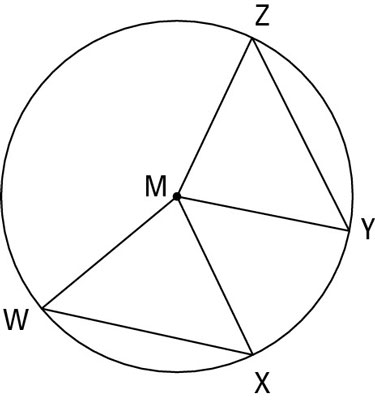
Central angles and arcs:
1. If two central angles of a circle (or of congruent circles) are congruent, then their intercepted arcs are congruent. (Short form: If central angles congruent, then arcs congruent.)
2. If two arcs of a circle (or of congruent circles) are congruent, then the corresponding central angles are congruent. (Short form: If arcs congruent, then central angles congruent.)
Central angles and chords:
3. If two central angles of a circle (or of congruent circles) are congruent, then the corresponding chords are congruent. (Short form: If central angles congruent, then chords congruent.)
4. If two chords of a circle (or of congruent circles) are congruent, then the corresponding central angles are congruent. (Short form: If chords congruent, then central angles congruent.)
Arcs and chords:
5. If two arcs of a circle (or of congruent circles) are congruent, then the corresponding chords are congruent. (Short form: If arcs congruent, then chords congruent.)
6. If two chords of a circle (or of congruent circles) are congruent, then the corresponding arcs are congruent. (Short form: If chords congruent, then arcs congruent.)
Here’s a more condensed way of thinking about the six theorems:
If the angles are congruent, both the chords and the arcs are congruent.
If the chords are congruent, both the angles and the arcs are congruent.
If the arcs are congruent, both the angles and the chords are congruent.
These three ideas condense further to one simple idea: If any pair (of central angles, chords, or arcs) is congruent, then the other two pairs are also congruent.






