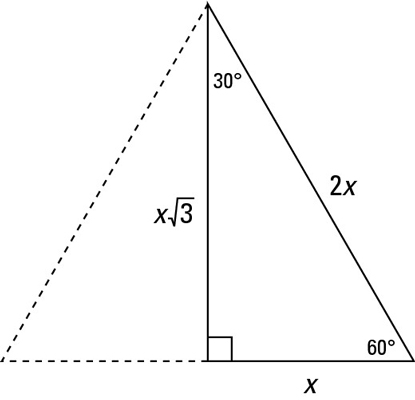
The 30 – 60 – 90 degree triangle is in the shape of half an equilateral triangle, cut straight down the middle along its altitude. It has angles of 30°, 60°, and 90° and sides in the ratio of
The following figure shows an example.
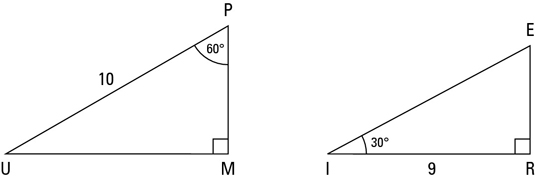
Get acquainted with this triangle by doing a couple of problems. Find the lengths of the unknown sides in triangle UMP and triangle IRE in the following figure.
You can solve 30°- 60°- 90° triangles with the textbook method or the street-smart method.
Using the textbook method
The textbook method begins with the ratio of the sides from the first figure:
In triangle UMP, the hypotenuse is 10, so you set 2x equal to 10 and solve for x, getting x = 5. Now just plug 5 in for the x’s, and you have triangle UMP:
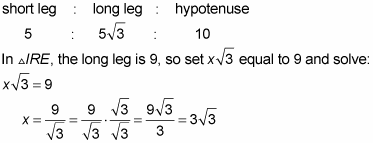
Plug in the value of x, and you’re done:
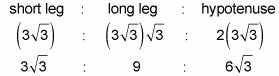
Using the street-smart method
Here’s the street-smart method for the 30°- 60°- 90° triangle.
Using that fact, do the following:
The relationship between the short leg and the hypotenuse is a no-brainer: the hypotenuse is twice as long as the short leg. So if you know one of them, you can get the other in your head.

If you know the short leg and want to compute the long leg (a longer thing), you multiply by the square root of 3. If you know the long leg and want to compute the length of the short leg (a shorter thing), you divide by the square root of 3.
Try out the street-smart method with the triangles in the second figure. The hypotenuse in triangle UMP is 10, so first you cut that in half to get the length of the short leg, which is thus 5.

The 30°- 60°- 90° triangles almost always have one or two sides whose lengths contain a square root. In either case, the long leg is the odd one out. All three sides could contain square roots, but it’s impossible that none of the sides would — which leads to the following warning.
Because at least one side of a 30°- 60°- 90° triangle must contain a square root, a 30°- 60°- 90° triangle cannot belong to any of the Pythagorean triple triangle families. So don’t make the mistake of thinking that a 30°- 60°- 90° triangle is in, say, the 8 : 15 : 17 family or that any triangle that is in one of the Pythagorean triple triangle families is also a 30°- 60°- 90° triangle. There’s no overlap between the 30°- 60°- 90° triangle and any of the Pythagorean triple triangles and their families.






