The Angle-Bisector theorem states that if a ray bisects an angle of a triangle, then it divides the opposite side into segments that are proportional to the other two sides. The following figure illustrates this.
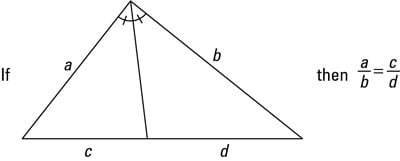
The Angle-Bisector theorem involves a proportion — like with similar triangles. But note that you never get similar triangles when you bisect an angle of a triangle (unless you bisect the vertex angle of an isosceles triangle, in which case the angle bisector divides the triangle into two congruent triangles).
Don’t forget the Angle-Bisector Theorem. (For some reason, students often do forget this theorem.) So whenever you see a triangle with one of its angles bisected, consider using the theorem.
How about an angle-bisector problem? Why? Oh, just BCUZ.
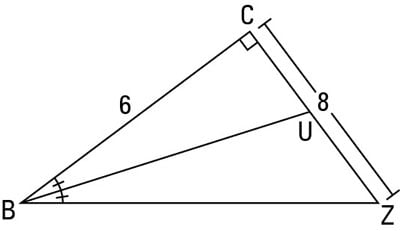
Given: Diagram as shown
Find: 1.) BZ, CU, UZ, and BU and 2.) The area of triangle BCU and triangle BUZ
Find BZ, CU, UZ, and BU.

It’s a 6-8-10 triangle, so BZ is 10.
Next, set CU equal to x. UZ then becomes 8 – x. Set up the angle-bisector proportion and solve for x:
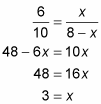
So CU is 3 and UZ is 5.
The Pythagorean Theorem then gives you BU:
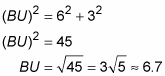
Calculate the area of triangle BCU and triangle BUZ.
Both triangles have a height of 6 (when you use segment CU and segment UZ as their bases), so just use the triangle area formula:
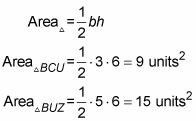
Note that the ratio of the areas of these triangles, 9 : 15 (which reduces to 3 : 5), is equal to the ratio of the triangles’ bases, 3 : 5. This equality holds whenever a triangle is divided into two triangles with a segment from one of its vertices to the opposite side (whether or not this segment cuts the vertex angle exactly in half).

