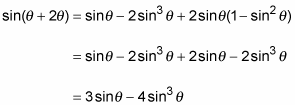Sum and difference identities usually involve two different angles and then a third combined angle. When proving these trig identities, you often need to get rid of that third angle. The following example involves a sum of two different angles.
-
Replace the cosine of the sum of the two angles with its identity.
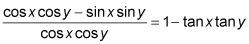
-
Break up the fraction by putting each term in the numerator over the denominator.
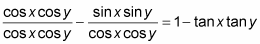
-
Reduce the first fraction. Rewrite the second fraction as the product of two fractions. Then replace the two fractions in that product by using the ratio identity.
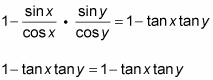
The next example shows an identity for three times an angle: sin3θ = 3sinθ – 4 sin3θ.
-
Replace the 3θ with the sum of θ and 2θ to create the identity for the sum of two angles.
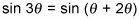
-
Apply the angle-sum identity for sine.
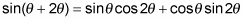
-
Now replace cos2θ and sin2θ by using the double-angle identities.
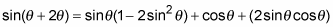
You have to choose the right identity for the cos2θ. In this example, you want the final result to be all sines of the same angle.
-
Multiply through on the right side.
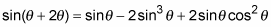
-
Replace cos2θ with its equivalent by using the Pythagorean identity. Then simplify the terms.